
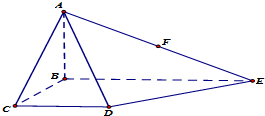
 如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.
如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.分析 (1)证明线面平面,转化为证明面面平行即可.点F为AE的中点,取BE中点G,连接FG,DG,证明平面FGD∥平面ABC;可得FD∥平面ABC.
(2)通过转化寻找AC与DE所成角平面角,连接GC,可得DE∥GC,那么异面直线AC与DE所成角为∠ACG,利用余弦定理求解即可.
解答 解:(1)点F为AE的中点,取BE中点G,连接FG,DG,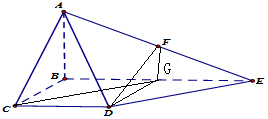
∴FG∥AB,
BE=2CD,CD∥BE,
∴BG${\;}_{∥}^{=}$CD,
∵∠BCD=90°
∴BCDG是正方形,DG∥BC.
又∵DG?平面FGD,FG?平面FGD,FG∩DG=G,FG∥AB,DG∥BC
∴平面FGD∥平面ABC;
∵FD?平面FGD
∴FD∥平面ABC;
(2)连接GC,BE=2CD,CD∥BE,
∴DE∥GC,
那么异面直线AC与DE所成角为∠ACG,
设AB=a,
∵BE=4AB=2BC=2CD,即BE=4a,BC=2a,CD=2a.
AB⊥底面BCDE,BCDG是正方形,
∴AC=$\sqrt{5}a$,GC=$2\sqrt{2}a$,AG=$\sqrt{5}a$.
在△ACG中,cos∠ACG=$\frac{A{C}^{2}+C{G}^{2}-A{G}^{2}}{2AC•CG}=\frac{\sqrt{10}}{5}$
∴异面直线AC与DE所成角的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查了线面平面,转化为证明面面平行以及异面直线所成角的证明及计算.属于中档题.


科目:高中数学 来源: 题型:填空题
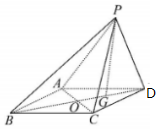 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量n | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数(天) | 10 | 20 | 20 | 14 | 13 | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com