
【题目】若一系列函数的解析式和值域相同,但其定义域不同,则称这些函数为“同族函数”,例如函数![]() 与函数
与函数![]() ,
,![]() 为“同族函数”.下面函数解析式中能够被用来构造“同族函数”的是( )
为“同族函数”.下面函数解析式中能够被用来构造“同族函数”的是( )
A.![]() B.
B.![]() C.
C.![]()
D.![]() E.
E.![]()
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b为何值时,ax2+bx+3≥0的解集为R.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种子培育基地新研发了![]() 两种型号的种子,从中选出90粒进行发芽试验,并根据结果对种子进行改良.将试验结果汇总整理绘制成如下
两种型号的种子,从中选出90粒进行发芽试验,并根据结果对种子进行改良.将试验结果汇总整理绘制成如下![]() 列联表:
列联表:

(1)将![]() 列联表补充完整,并判断是否有99%的把握认为发芽和种子型号有关;
列联表补充完整,并判断是否有99%的把握认为发芽和种子型号有关;
(2)若按照分层抽样的方式,从不发芽的种子中任意抽取20粒作为研究小样本,并从这20粒研究小样本中任意取出3粒种子,设取出的![]() 型号的种子数为
型号的种子数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+(a+4)x+lnx.
(1)若f(x)在x= ![]() 处的切线与直线4x+y=0平行,求a的值;
处的切线与直线4x+y=0平行,求a的值;
(2)讨论函数f(x)的单调区间;
(3)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0 , 证明f′(x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.函数
单调递增.函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间;(只写结论,不需证明)
的单调区间;(只写结论,不需证明)
(2)求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)讨论方程![]() 实根的个数.
实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规则是:先后掷两枚骰子,将此试验重复n轮,第n轮的点数分别记为xn , yn , 如果点数满足xn< ![]() ,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(Ⅰ)求第一轮闯关成功的概率;
(Ⅱ)如果第i轮闯关成功所获的奖金数f(i)=10000× ![]() (单位:元),求某人闯关获得奖金不超过1250元的概率;
(单位:元),求某人闯关获得奖金不超过1250元的概率;
(Ⅲ)如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量X,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设![]() 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
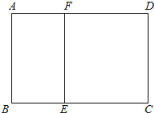
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com