练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，四面体ABCD被一平面所截，截面与四条棱AB、AC、CD、BD相交于E、F、G、H四点，且截面EFGH是一个平行四边形.

    求证：棱BC∥平面EFGH，AD∥平面EFGH.

    思路解析：依据判定定理，在平面EFGH内寻找与BC、AD平行的直线，利用线面平行的性质即得.

    证明：因为截面EFGH是一个平行四边形，所以EF∥GH.

    又因为GH在平面DCB内，EF不在平面DCB内，所以EF∥平面DCB.

    又平面ABC过直线EF且与平面DCB相交于BC.

    所以EF∥BC，EF?面EFGH.

    所以BC∥平面EFGH.

    同理，可证AD∥平面EFGH.

    方法归纳  反复运用线面平行的判定定理和性质定理，实现线面平行与线线平行的相互转化，在同一道题中是常用的.

    巧妙变式  若将本题中E、F、G、H特殊化，即E、F、G、H分别是AB、AC、DC、DB的中点，可由对应线段成比例推证平行，转化为利用三角形的中位线定理证直线平行，然后证明本题的结论成立.

    证明：∵E、F分别是AB、AC的中点，∴EF*BC.

    同理，∵G、H分别是DC、DB的中点，

    ∴GH*BC.


    ∴EF*GH.

    ∴四边形EFGH是平行四边形(以下证法同上).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

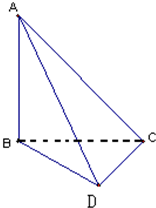    精英家教网在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1．
    （Ⅰ）求证：平面ACD⊥平面ABC；
    （Ⅱ）求二面角C-AB-D的大小；
    （Ⅲ）若直线BD与平面ACD所成的角为30°，求线段AB的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

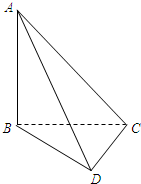    （2009•襄阳模拟）在如图所示的四面体ABCD中，AB、BC、CD两两互相垂直，且BC=CD=1．
    （1）求证：平面ACD⊥平面ABC；
    （2）求二面角C-AB-D的大小；
    （3）若直线BD与平面ACD所成的角为θ，求θ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•河东区二模）如图所示，四面体ABCD中，O、E分别是BD和BC的中点，且AB=AD=
    		2
    ，AC=BC=CD=BD=2
    （1）求证：AO⊥平面BCD；
    （2）求三棱锥E-ACD的体积．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年河南省原名校高三下学期第二次联考理科数学试卷（解析版） 题型：解答题

    如图所示，四面体ABCD中，AB⊥BD、AC⊥CD且AD =3．BD=CD=2．

    （1）求证：AD⊥BC；

    （2）求二面角B—AC—D的余弦值．

     

    查看答案和解析>>

    同步练习册答案