
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如表的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求y关于x的回归直线方程;(参考公式: ![]() =
= 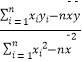 ,
, ![]() =y﹣
=y﹣ ![]() )
)
(2)已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大?(利润=售价﹣收购价)
【答案】
(1)解:由已知: ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 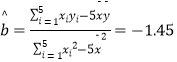 ,
,
![]()
所求线性回归直线方程为 ![]()
(2)解:L(x)=y﹣w=﹣1.45x+18.7﹣(0.01x3﹣0.09x2﹣1.45x+17.2)=﹣0.01x3+0.09x2+1.5(0<x≤10)
L′(x)=﹣0.03x2+0.18x=﹣0.03x(x﹣6)
x∈(0,6)时,L′(x)>0,L(x)单调递增,x∈(6,10]时,L′(x)<0,L(x)单调递减
所以预测x=6时,销售一辆该型号汽车所获得的利润L(x)最大.
【解析】(1)由表中数据计算b,a,即可写出回归直线方程;(2)写出利润函数L(x)=y﹣w,利用导数求出x=6时L(x)取得最大值.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E , F分别为棱AB , CC1的中点,则在平面ADD1A1内且与平面D1EF平行的直线( )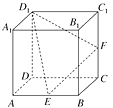
A.不存在
B.有1条
C.有2条
D.有无数条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立,则实数a的取值范围是( )
A.(﹣∞,1]
B.[0,1]
C.![]()
D.[0,e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数满足x2﹣4ax+3a2<0,a≠0;命题q:实数满足 ![]() ≥0.
≥0.
(1)若a=1,p∧q为真命题,求x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a2x﹣2﹣x定义域为R的奇函数.
(1)求实数a的值;
(2)判断函数f(x)在R上的单调性,并利用函数单调性的定义证明;
(3)若不等式f(9x+1)+f(t﹣23x+5)>0在在R上恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com