
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3(a>0且a≠1).
x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+1(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=lnx![]() ,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
,若对任意的x1∈(0,+∞),存在x2∈(1,+∞),使得f(x1)<g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]() 对一切
对一切![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(3)设数列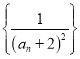 的前n项和为
的前n项和为![]() ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道(![]() )和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
)和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“非常满意”的观众的概率为0.35.
地区当中“非常满意”的观众的概率为0.35.
非常满意 | 满意 | 合计 | |
| 30 | 15 | |
|
|
| |
合计 |
(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“非常满意”的![]() 、
、![]() 地区的人数各是多少.
地区的人数各是多少.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.
(3)若以抽样调查的频率为概率,从![]() 地区随机抽取3人,设抽到的观众“非常满意”的人数为
地区随机抽取3人,设抽到的观众“非常满意”的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:参考公式:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com