
【题目】在平面直角坐标系中,圆![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .以
.以![]() 为顶点,
为顶点,![]() 分别为左、右焦点的椭圆
分别为左、右焦点的椭圆![]() ,恰好经过点
,恰好经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() (2)当直线
(2)当直线![]() 的斜率为
的斜率为![]() 时,可使
时,可使![]() 的面积最大,其最大值
的面积最大,其最大值![]() .
.
【解析】试题分析:
(1)由已知可得,椭圆![]() 的焦点在
的焦点在![]() 轴上.设椭圆
轴上.设椭圆![]() 的标准方程为
的标准方程为![]() ,易知
,易知![]() ,结合椭圆过点
,结合椭圆过点![]() ,可得椭圆
,可得椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意可知直线![]() 的斜率存在.设直线方程为
的斜率存在.设直线方程为![]() ,
,![]() .联立直线方程与椭圆方程有
.联立直线方程与椭圆方程有![]() .直线与椭圆交于不同的两点,则
.直线与椭圆交于不同的两点,则![]() ,
,![]() ,由弦长公式可得
,由弦长公式可得![]() ,而点
,而点![]() 到直线
到直线![]() 的距离
的距离![]() ,据此可得面积函数
,据此可得面积函数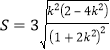 .换元令
.换元令![]() ,
,![]() ,结合二次函数的性质可得当直线
,结合二次函数的性质可得当直线![]() 的斜率为
的斜率为![]() 时,可使
时,可使![]() 的面积最大,其最大值
的面积最大,其最大值![]() .
.
试题解析:
(1)由已知可得,椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
设椭圆![]() 的标准方程为
的标准方程为![]() ,焦距为
,焦距为![]() ,则
,则![]() ,
,
∴![]() ,∴椭圆
,∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
又∵椭圆![]() 过点
过点![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由于点![]() 在椭圆
在椭圆![]() 外,所以直线
外,所以直线![]() 的斜率存在.
的斜率存在.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() ,设
,设![]() .
.
由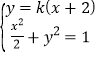 消去
消去![]() 得,
得,![]() .
.
由![]() 得
得![]() ,从而
,从而![]() ,
,
∴![]() .
.
∵点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() 的面积为
的面积为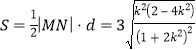 .
.
令![]() ,则
,则![]() ,
,
∴![]()
![]() ,
,
当![]() 即
即![]() 时,
时,![]() 有最大值,
有最大值,![]() ,此时
,此时![]() .
.
所以,当直线![]() 的斜率为
的斜率为![]() 时,可使
时,可使![]() 的面积最大,其最大值
的面积最大,其最大值![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是 ( )
A. (x-1)2+y2=2 B. (x+1)2+y2=2 C. (x-1)2+y2=4 D. (x+1)2+y2=4
【答案】A
【解析】圆![]() 的标准方程为
的标准方程为![]() ,所以圆心为(0,1),半径为
,所以圆心为(0,1),半径为![]() ,圆心关于直线
,圆心关于直线![]() 的对称点是(1,0),所以圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是
的对称点是(1,0),所以圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是![]() ,选A.
,选A.
点睛:本题主要考查圆关于直线的对称的圆的方程,属于基础题。解答本题的关键是求出圆心关于直线的对称点,两圆半径相同。
【题型】单选题
【结束】
8
【题目】已知双曲线的离心率为![]() ,焦点是
,焦点是![]() ,
, ![]() ,则双曲线方程为 ( )
,则双曲线方程为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 关于坐标轴对称,以坐标原点
关于坐标轴对称,以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,
轴的正半轴为极轴建立极坐标系, ![]() ,
, ![]() 为椭圆
为椭圆![]() 上两点.
上两点.
(1)求直线![]() 的直角坐标方程与椭圆
的直角坐标方程与椭圆![]() 的参数方程;
的参数方程;
(2)若点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在第一象限内,求四边形
在第一象限内,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某中学举行的物理知识竞赛中,将三个年级参赛学生的成绩在进行整理后分成5组,绘制出如图所示的须率分布直方图,图中从左到右依次为第一、第二、第三、第四、第五小组.已知第三小组的频数是15.

(1)求成绩在50-70分的频率是多少
(2)求这三个年级参赛学生的总人数是多少:
(3)求成绩在80-100分的学生人数是多少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的一段图象如图所示.
的一段图象如图所示.
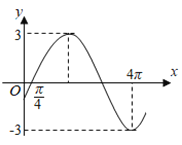
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调减区间,并指出
的单调减区间,并指出![]() 的最大值及取到最大值时
的最大值及取到最大值时![]() 的集合;
的集合;
(3)把![]() 的图象向右至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
的图象向右至少平移多少个单位,才能使得到的图象对应的函数为偶函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段AB的端点B的坐标为(3,0),端点A在圆![]() 上运动;
上运动;
(1)求线段AB中点M的轨迹方程;
(2)过点C(1,1)的直线m与M的轨迹交于G、H两点,求以弦GH为直径的圆的面积最小值及此时直线m的方程.
(3)若点C(1,1),且P在M轨迹上运动,求![]() 的取值范围.(O为坐标原点)
的取值范围.(O为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用随机数表对生产的600个零件进行抽样测试,先将600个零件进行编号,编号分别为001,002,![]() ,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
,599,600从中抽取60个样本,如下提供随机数表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若从表中第6行第6列开始向右依次读取3个数据,则得到的第6个样本编号![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过平面直角坐标系中的点P(4-3a,![]() )(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积
)(a∈R)作圆x2+y2=1的两条切线PA,PB,切点分别为A,B,则数量积![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com