
【题目】棱长为2的正方体在平面![]() 上的射影的面积最大值等于________________.
上的射影的面积最大值等于________________.
【答案】![]()
【解析】
对正方体而言,无论从外部那个角度看,最多只能看到三个面,所以可只考虑共顶点的三个面在某一个平面上的射影的面积的最值就就足够了,正方体共顶点在平面![]() 上的射影的面积记为
上的射影的面积记为![]() ,这三个平面与平面
,这三个平面与平面![]() 所成二面角分别记为
所成二面角分别记为![]() ,则
,则
![]() ,可证
,可证![]() ,利用基本不等式,可求出
,利用基本不等式,可求出![]() 的最大值,即可得出结论.
的最大值,即可得出结论.
先推导一个结论:
三棱锥![]() 的三条侧棱
的三条侧棱![]() 两两互相垂直,
两两互相垂直,
三侧面与底面所成的二面角分别记为![]() ,则有
,则有
![]() 成立,以下证明:
成立,以下证明:
如图,![]() 是
是![]() 在底面
在底面![]() 上的射影,
上的射影,
连![]() 并延长分别交三边于
并延长分别交三边于![]() ,
,
连![]() ,
,![]() 两两互相垂直,
两两互相垂直,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 是二面角
是二面角![]() 的平面角,记为
的平面角,记为![]() ,
,
同理另两侧面与底面所成二面角分别为![]()
记为![]() ,三侧面
,三侧面![]() 及底面
及底面![]() 的面积分别记为
的面积分别记为
![]() 平面
平面![]() ,
,![]() (射影面积公式),
(射影面积公式),
同理![]() ,①
,①
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,②
,②
①代入②,![]() ;
;
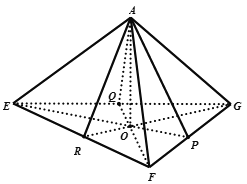
正方体的边长为2,每个面的面积为4,
正方体共顶点在平面![]() 上的射影的面积记为
上的射影的面积记为![]() ,
,
这三个平面与平面![]() 所成二面角分别记为
所成二面角分别记为![]() ,则
,则
![]() ,
,
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() ,等号成立,
,等号成立,
正方体在平面![]() 上的射影是如下图所示的正六边形,其面积最大为
上的射影是如下图所示的正六边形,其面积最大为![]() .
.
故答案为:![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
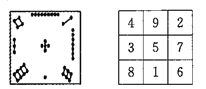
【题目】我国古代的《洛书》中记载着世界上最古老的一个幻方:如图,将1,2,…,9填入![]() 的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数
的方格内,使三行,三列和两条对角线上的三个数字之和都等于15.一般地,将连续的正整数![]() 填入
填入![]() 个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做
个方格中,使得每行,每列和两条对角线上的数字之和都相等,这个正方形叫做![]() 阶幻方.记
阶幻方.记![]() 阶幻方的对角线上的数字之和为
阶幻方的对角线上的数字之和为![]() ,如图三阶幻方的
,如图三阶幻方的![]() ,那么
,那么![]() 的值为__________ .
的值为__________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出命题:(1)对立事件一定是互斥事件.(2)若事件![]() 满足
满足![]() ,则
,则![]() 为对立事件.(3)把
为对立事件.(3)把![]() 、
、![]() 、
、![]() ,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件
,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件![]() :“甲得红桃
:“甲得红桃![]() ”与事件
”与事件![]() :“乙得红桃
:“乙得红桃![]() ”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
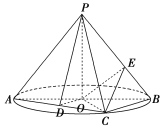
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
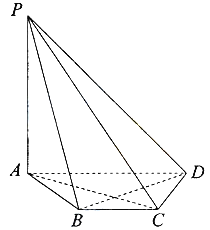
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() 成等比数列.数列
成等比数列.数列![]() 满足:
满足:![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且 ,若对
,若对![]() ,
,![]() 恒成立,求正整数k的值.
恒成立,求正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司结合公司的实际情况针对调休安排展开问卷调查,提出了A,B,C三种放假方案,调查结果如下:

(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com