练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．求证：$\frac{1+sin4θ-cos4θ}{1+sin4θ+cos4θ}$=tan2θ

    分析 从左边入手，利用三角函数的倍角公式对分子、分母分别化简约分，得到证明．

    解答 证明：左边=$\frac{2si{n}^{2}2θ+2sin2θcos2θ}{2co{s}^{2}2θ+2sin2θcos2θ}$=$\frac{2sin2θ（sin2θ+cos2θ）}{2cos2θ（cos2θ+sin2θ）}$=$\frac{sin2θ}{cos2θ}$=tan2θ=右边．

    点评 本题考查了三角恒等式的证明；用到了三角函数的倍角公式、基本关系式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．设集合M={a2-a，0}．若a∈M，则实数a的值为（　　）
    A．0B．2C．2或0D．2或-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．有红、黄、蓝、白4种颜色的小球，每种小球数量不限且它们除颜色不同外，其余完全相同，将小球放入如图所示编号为1，2，3，4，5的盒子中，每个盒子只放一只小球．
    （1）放置小球满足：“对任意的正整数j（1≤j≤5），至少存在另一个正整数k（1≤k≤5，且j≠k）使得j号盒子与k号盒子中所放小球的颜色相同”的概率；
    （2）记X为5个盒子中颜色相同小球个数的最大值，求X的概率分布和数学期望E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．如果对于任意实数a，b（a＜b），随机变量X满足P（a＜X≤b）=${∫}_{a}^{b}$φμσ（x）dx，称随机变量X服从正态分布，记为N（μ，σ2），若X～N（0，1），则${∫}_{-1}^{1}$φμσ（x）dx=0.6826．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知f（x）=$\frac{lnx}{1+x}$，f（x）在x=x0处取得最大值，以下各式正确的序号为①④
    ①f（x0）＜x0；   ②f（x0）=x0；  ③f（x0）＞x0；
    ④f（x0）＜$\frac{1}{2}$；   ⑤f（x0）＞$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某市工业部门计划对所辖中小型工业企业推行节能降耗技术改造，对所辖企业是否支持改造进行问卷调查，结果如表：
    支持不支持合计
    中型企业8040120
    小型企业240200440
    合计320240560
    （1）从上述320家支持节能降耗改造的中小企业中按分层抽样的方法抽出8家，中小型企业各应抽几家？
    （2）能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关？
    P（K2≥k0）0.0500.0250.010
    k03.8415.0246.635
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数y=xlnx在区间（　　）
    A．（0，+∞）上单调递减B．$（\frac{1}{e}，+∞）$上单调递减C．$（0，\frac{1}{e}）$上单调递减D．（0，+∞）上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．若A，B，C，D，E，F六个不同元素排成一列，要求A不排在两端，且B、C相邻，则不同的排法共有144种（用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

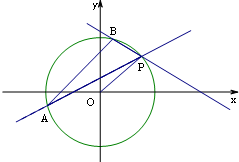    7．已知圆C过点p（1，1），且与圆M：（x+2）2+（y+2）2=r2（r＞0）关于直线x+y+2=0对称．
    （1）求圆C的方程．
    （2）过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，求证：直线OP与直线AB平行．

    查看答案和解析>>

    同步练习册答案