
【题目】2019新型冠状病毒感染的肺炎的传播有飞沫、气溶胶、接触等途径,为了有效抗击疫情,隔离性防护是一项具体有效措施.某市为有效防护疫情,宣传居民尽可能不外出,鼓励居民的生活必需品可在网上下单,商品由快递业务公司统一配送(配送费由政府补贴).快递业务主要由甲公司与乙公司两家快递公司承接:“快递员”的工资是“底薪+送件提成”.这两家公司对“快递员”的日工资方案为:甲公司规定快递员每天底薪为70元,每送件一次提成1元;乙公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成5元,假设同一公司的快递员每天送件数相同,现从这两家公司往年忙季各随机抽取一名快递员并调取其100天的送件数,得到如下条形图:

(1)求乙公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题:
①记甲公司的“快递员”日工资为X(单位:元).求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
【答案】(1)![]() ;(2)①分布列详见解析,数学期望为156.8元;②小王应当到甲公司应聘“快递员”的工作,理由详见解析.
;(2)①分布列详见解析,数学期望为156.8元;②小王应当到甲公司应聘“快递员”的工作,理由详见解析.
【解析】
(1)根据题意分![]() 与
与![]() 两段求出一日工资y(单位:元)与送件数n的函数关系即可.
两段求出一日工资y(单位:元)与送件数n的函数关系即可.
(2)①根据送件数以及(1)中的函数可知X的所有可能取值为152,154,156,158,160.在结合图中各送件数的频数求出对应的频率,继而求得分布列与数学期望即可.
②分别求出两家公司送餐日工资的数学期望,比较大小再判定即可.
(1)由题意:当![]() 时,
时,![]() 元;
元;
当![]() 时,
时,![]() .
.
∴乙公司的快递员一日工资y(单位:元)与送件数n的函数关系为:
![]()
(2)①X的所有可能取值为152,154,156,158,160.
由题可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∴X的分布列为:
X | 152 | 154 | 156 | 158 | 160 |
P | 0.1 | 0.2 | 0.1 | 0.4 | 0.2 |
X的数学期望![]() (元)
(元)
②设乙公司的日工资为Y,
则![]() (元)
(元)
由于到甲公司的日工资的数学期望(均值)比乙公司的日工资的数学期望(均值)高,
所以小王应当到甲公司应聘“快递员”的工作.


科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an}的前n项和为Sn,S3=15,a1,a4,a13成等比数列.
(1)求数列{an}的通项公式;
(2)求数列![]() 的前n项和Tn大于2020的最小自然数n.
的前n项和Tn大于2020的最小自然数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
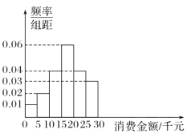
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】笔、墨、纸、砚是中国独有的文书工具,即“文房四宝”.笔、墨、纸、砚之名,起源于南北朝时期,其中的“纸”指的是宣纸,宣纸“始于唐代,产于泾县”,而唐代泾县隶属于宣州府管辖,故因地而得名“宣纸”,宣纸按质量等级,可分为正牌和副牌(优等品和合格品),某公司年产宣纸10000刀,公司按照某种质量标准值x给宣纸确定质量等级,如表所示:
x | (48,52] | (44,48]∪(52,56] | (0,44]∪(56,100] |
质量等级 | 正牌 | 副牌 | 废品 |
公司在所生产的宣纸中随机抽取了一刀(100张)进行检验,得到频率分布直方图如图所示,已知每张正牌纸的利润是10元,副牌纸的利润是5元,废品亏损10元.

(Ⅰ)按正牌、副牌、废品进行分层抽样,从这一刀(100张)纸中抽出一个容量为5的样本,再从这个样本中随机抽出两张,求其中无废品的概率;
(Ⅱ)试估计该公司生产宣纸的年利润(单位:万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣HKLE中,底面ABCD是边长为3的正方形,对角线AC与BD相交于点O,点F在线段AH上且![]() ,BE与底面ABCD所成角为
,BE与底面ABCD所成角为![]() .
.
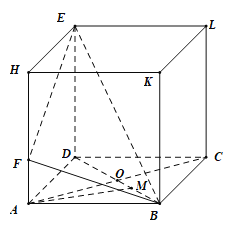
(1)求证:AC⊥BE;
(2)M为线段BD上一点,且![]() ,求异面直线AM与BF所成角的余弦值.
,求异面直线AM与BF所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() =(cosx,sinx),
=(cosx,sinx),![]() =(cosx,﹣sinx),函数
=(cosx,﹣sinx),函数![]() .
.
(1)若![]() ,x
,x![]() (0,
(0,![]() ),求tan(x+
),求tan(x+![]() )的值;
)的值;
(2)若![]() ,
,![]() (
(![]() ,
,![]() ),
),![]() ,
,![]() (0,
(0,![]() ),求
),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com