
【题目】[选修4-5:不等式选讲]
设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0).
|+|x﹣2m|(m>0).
(Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
【答案】(Ⅰ)证明:函数f(x)=|x+ ![]() |+|x﹣2m|(m>0),
|+|x﹣2m|(m>0),
∴f(x)=|x+ ![]() |+|x﹣2m|≥|x+
|+|x﹣2m|≥|x+ ![]() ﹣(x﹣2m)|=|
﹣(x﹣2m)|=| ![]() +2m|=
+2m|= ![]() +2m≥2
+2m≥2 ![]() =8,
=8,
当且仅当m=2时,取等号,故f(x)≥8恒成立.
(Ⅱ)f(1)=|1+ ![]() |+|1﹣2m|,当m>
|+|1﹣2m|,当m> ![]() 时,f(1)=1+
时,f(1)=1+ ![]() ﹣(1﹣2m),不等式即
﹣(1﹣2m),不等式即 ![]() +2m>10,
+2m>10,
化简为m2﹣5m+4>0,求得m<1,或m>4,故此时m的范围为( ![]() ,1)∪(4,+∞).
,1)∪(4,+∞).
当0<m≤ ![]() 时,f(1)=1+
时,f(1)=1+ ![]() +(1﹣2m)=2+
+(1﹣2m)=2+ ![]() ﹣2m关于变量m单调递减,
﹣2m关于变量m单调递减,
故当m= ![]() 时,f(1)取得最小值为17,
时,f(1)取得最小值为17,
故不等式f(1)>10恒成立.
综上可得,m的范围为(0,1)∪(4,+∞).
【解析】(Ⅰ)利用绝对值三角不等式、基本不等式证得f(x)≥8恒成立.
(Ⅱ)当m> ![]() 时,不等式即
时,不等式即 ![]() +2m>10,即m2﹣5m+4>0,求得m的范围.当0<m≤
+2m>10,即m2﹣5m+4>0,求得m的范围.当0<m≤ ![]() 时,f(1)=1+
时,f(1)=1+ ![]() +(1﹣2m)=2+
+(1﹣2m)=2+ ![]() ﹣2m关于变量m单调递减,求得f(1)的最小值为17,可得不等式f(1)>10恒成立.综合可得m的范围.
﹣2m关于变量m单调递减,求得f(1)的最小值为17,可得不等式f(1)>10恒成立.综合可得m的范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}是公差大于0的等差数列,Sn为数列{an}的前n项和,已知S3=9,且2a1 , a3﹣1,a4+1构成等比数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() =2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
=2n﹣1(n∈N*),设Tn是数列{bn}的前n项和,证明:Tn<6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣alnx(a∈R)
x2﹣alnx(a∈R)
(1)若函数f(x)在x=2处的切线方程为y=x+b,求a,b的值;
(2)讨论方程f(x)=0解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;
(Ⅲ)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.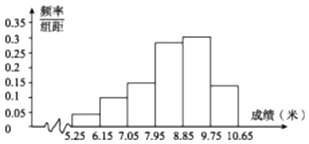
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为菱形,E为AC与BD的交点,PA⊥平面ABCD,M为PA中点,N为BC中点. 
(1)证明:直线MN∥平面PCD;
(2)若点Q为PC中点,∠BAD=120°,PA= ![]() ,AB=1,求三棱锥A﹣QCD的体积.
,AB=1,求三棱锥A﹣QCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种, 方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2xlnx﹣x2+2ax,其中a>0.
(1)设g(x)是f(x)的导函数,求函数g(x)的极值;
(2)是否存在常数a,使得x∈[1,+∞)时,f(x)≤0恒成立,且f(x)=0有唯一解,若存在,求出a的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com