
【题目】已知函数![]() ,
, ![]() 是
是![]() 的导函数.
的导函数.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() 在
在![]() 时取得最小值,求
时取得最小值,求![]() 的取值范围;
的取值范围;
(3)在(1)的条件下,当![]() 时,
时, ![]() .
.
【答案】(1)a=-1;(2)[0,1];(3)见解析.
【解析】试题分析:(1)根据![]() ,即可得结果;(2)分三种情况分别求函数的最小值,分别验证是否
,即可得结果;(2)分三种情况分别求函数的最小值,分别验证是否![]() 在
在![]() 时取得最小值,即可得结果;(3)利用导数研究函数的单调性,分两种情况分别利用分析法证明即可.
时取得最小值,即可得结果;(3)利用导数研究函数的单调性,分两种情况分别利用分析法证明即可.
试题解析:(1)f(x)=x-asinx,f(![]() )=
)=![]() -a=
-a=![]() 所以a=-1,经验证a=-1合题意;
所以a=-1,经验证a=-1合题意;
(2)g(x)= f(x)= x-asinx g(x)=1-acosx
①当a=0时, f(x)=![]() x2,显然在x=0时取得最小值, ∴a=0合题意;
x2,显然在x=0时取得最小值, ∴a=0合题意;
②当a>0时,
(i)当![]() ≥1即0<a≤1时, g(x)≥0恒成立, ∴g(x)在(-∞,+∞)上单调递增,又g(0)=0
≥1即0<a≤1时, g(x)≥0恒成立, ∴g(x)在(-∞,+∞)上单调递增,又g(0)=0
∴当x<0时,g(x)<0 即f(x)<0, 当x>0时,g(x)>0 即f(x)>0
∴f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增;
∴f(x) 在x=0时取得最小值
∴当0<a≤1时合题意;
(ii)当0<![]() <1即a>1时,在(0,)内存在唯一x0=arccos
<1即a>1时,在(0,)内存在唯一x0=arccos![]() 使g(x)=0
使g(x)=0
当x(0,x0)时, ∵y=cosx在(0,)上是单调递减的, ∴cosx>cosx0=![]()
∴g(x)= a (![]() -cosx)<0 ∴g(x) 在(0, x0)上单调递减 ∴g(x)<g(0)=0
-cosx)<0 ∴g(x) 在(0, x0)上单调递减 ∴g(x)<g(0)=0
即f(x)<0 ∴f(x)在(0, x0)内单调递减;
∴x(0,x0)时,f(x)<0 这与f(x)在x=0时取得最小值即f(x)≥f(0)矛盾
∴当a>1时不合题意;
综上, a的取值范围是[0,1].
(3)由(1)知,a=-1 此时g(x)= x+sinx, g(x)=1+cosx
∴![]() =
=![]() =|cos
=|cos![]() |≥cos
|≥cos![]()
∴若要证原不等式成立,只需证cos![]() +
+![]() x2>
x2>![]() 成立;
成立;
由(2)知,当a=1时,f(x)≥f(0)恒成立,即![]() x2+cosx≥1恒成立
x2+cosx≥1恒成立
即cosx≥1-![]() x2(当且仅当x=0时取"="号)
x2(当且仅当x=0时取"="号)
∴cos![]() ≥1-
≥1-![]() x2(当且仅当x=0时取"="号) ……………①
x2(当且仅当x=0时取"="号) ……………①
∴只需证: 1-![]() x2+
x2+![]() x2>
x2>![]() 成立,即1+
成立,即1+![]() x2>
x2>![]()
又由均值不等式知:1+![]() x2≥x(当且仅当x=2时取"="号) ……………②
x2≥x(当且仅当x=2时取"="号) ……………②
∵①②两个不等式取"="的条件不一致
∴只需证: x≥![]()
两边取对数得:lnx≥1-![]() ……………③
……………③
下面证③式成立:令(x)=lnx-1+![]()
则(x)= ![]() -
-![]() =
=![]() ∴(x)在(0,1)上单调递减,在(1,+∞)上单调递增
∴(x)在(0,1)上单调递减,在(1,+∞)上单调递增
∴(x)≥(1)=0
即lnx-1+![]() ≥0 ∴lnx≥1-
≥0 ∴lnx≥1-![]()
即③式成立
∴原不等式成立


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
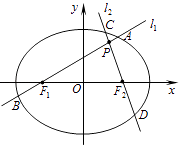
【题目】分别过椭圆E: ![]() =1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2
=1(a>b>0)左、右焦点F1、F2的动直线l1、l2相交于P点,与椭圆E分别交于A、B与C、D不同四点,直线OA、OB、OC、OD的斜率分别为k1、k2、k3、k4 , 且满足k1+k2=k3+k4 , 已知当l1与x轴重合时,|AB|=2 ![]() ,|CD|=
,|CD|= ![]() .
. 
(1)求椭圆E的方程;
(2)是否存在定点M,N,使得|PM|+|PN|为定值?若存在,求出M、N点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+ax﹣12=0},B={x|x2+bx+c=0},且A≠B,A∪B={﹣3,4},A∩B={﹣3},求实数b,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是BC的中点. 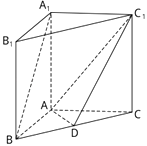
(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD﹣A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的两个焦点为![]() ,
, ![]() 是椭圆上一点,若
是椭圆上一点,若![]() ,
, ![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过右焦点
过右焦点![]() (不与
(不与![]() 轴重合)且与椭圆相交于不同的两点
轴重合)且与椭圆相交于不同的两点![]() ,在
,在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() 的值为定值?若存在,写出
的值为定值?若存在,写出![]() 点的坐标(不必求出定值);若不存在,说明理由.
点的坐标(不必求出定值);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为![]() .经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
.经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放.
某厂现有![]() 个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
个标准水量的A级水池,分别取样、检测. 多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若![]() ,求
,求![]() 个A级水样本混合化验结果不达标的概率;
个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若![]() ,现有
,现有![]() 个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5);求:
(1)求以向量 ![]() 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
(2)若向量a分别与向量 ![]() 垂直,且|a|=
垂直,且|a|= ![]() ,求向量a的坐标.
,求向量a的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为对数函数,并且它的图象经过点(2 ![]() ,
, ![]() ),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
),g(x)=[f(x)]2﹣2bf(x)+3,其中b∈R.
(1)求函数f(x)的解析式;
(2)求函数y=g(x)在区间[ ![]() ,16]上的最小值.
,16]上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com