
【题目】在平面直角坐标系中,已知三个点列{An}、{Bn}、{Cn},其中An(n,an)、Bn(n,bn)、Cn(n﹣1,0),满足向量 ![]() 与向量
与向量 ![]() 共线,且bn+1﹣bn=6,a1=b1=0,则an=(用n表示)
共线,且bn+1﹣bn=6,a1=b1=0,则an=(用n表示)
【答案】3n2﹣9n+6.3n2﹣9n+6(n∈N*)
【解析】解:∵bn+1﹣bn=6,a1=b1=0,
∴bn=0+6(n﹣1)=6n﹣6.
向量 ![]() =(1,an+1﹣an),
=(1,an+1﹣an),
向量 ![]() =(﹣1,﹣bn),
=(﹣1,﹣bn),
∵向量 ![]() 与向量
与向量 ![]() 共线,
共线,
∴﹣bn+an+1﹣an=0,
∴an+1﹣an=bn=6n﹣6,
∴an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1
=[6(n﹣1)﹣6]+[6(n﹣2)﹣6]+…+[6×1﹣6]+0
= ![]() ﹣6(n﹣1)
﹣6(n﹣1)
=3n2﹣9n+6.3n2﹣9n+6(n∈N*)
【考点精析】关于本题考查的向量的三角形法则,需要了解三角形加法法则的特点:首尾相连;三角形减法法则的特点:共起点,连终点,方向指向被减向量才能得出正确答案.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=  ,若存在实数x1 , x2 , x3 , x4满足f(xl)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则x1x2x3x4的取值范围是
,若存在实数x1 , x2 , x3 , x4满足f(xl)=f(x2)=f(x3)=f(x4),且x1<x2<x3<x4 , 则x1x2x3x4的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲罐中有3个红球,2个白球和3个黑球,乙罐中有5个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以![]() ,
,![]() 和
和![]() 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以![]() 表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号).
表示由乙罐取出的球是红球的事件,则下列结论中正确的是__________(写出所有正确结论的序号).
①P(B)=![]() ;②
;②![]() ;
;
③事件B与事件A1相互独立;
④A1,A2,A3是两两互斥的事件;
⑤P(B)的值不能确定,因为它与A1,A2,A3中究竟哪一个发生有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们休闲方式的一次调查中,其中主要休闲方式的选择有看电视和运动,现共调查了100人,已知在这100人中随机抽取1人,抽到主要休闲方式为看电视的人的概率为![]() 。
。
(1)完成下列2×2列联表;
休闲方式为看电视 | 休闲方式为运动 | 合计 | |
女性 | 40 | ||
男性 | 30 | ||
合计 |
(2)请判断是否可以在犯错误的概率不超过0.005的前提下认为性别与休闲方式有关系?
参考公式![]()
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 |
k | 1.323 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在定义域[﹣1,1]是奇函数,当x∈[﹣1,0]时,f(x)=﹣3x2 .
(1)当x∈[0,1],求f(x);
(2)对任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产的甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克) 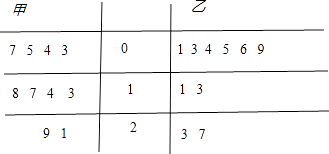
规定:当食品中的有害微量元素含量在[0,10]时为一等品,在(10,20]为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个.求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元.根据上表统计得到的甲、乙两种食品为一等品、二等品、劣质品,的频率分别估计这两种食品为,一等品、二等品、劣质品的概率.若分别从甲、乙食品中各抽取l件,设这两件食品给该厂带来的盈利为X,求随机变量X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)讨论函数f(x)的单调区间;
(2)当m≥ ![]() 时,设g(x)=2f(x)+x2的两个极值点x1 , x2(x1<x2)恰为h(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)h′(
时,设g(x)=2f(x)+x2的两个极值点x1 , x2(x1<x2)恰为h(x)=lnx﹣cx2﹣bx的零点,求y=(x1﹣x2)h′( ![]() )的最小值.
)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCDA1B1C1D1中,O为底面ABCD的中心,P,Q分别为![]() 的中点.
的中点.
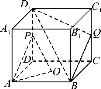
求证:(1)平面D1 BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 则一定有( )
则一定有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】本题主要考查不等关系。已知![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 。故选
。故选![]()
【题型】单选题
【结束】
5
【题目】关于x的不等式ax2+bx+2>0的解集为{x|-1<x<2},则关于x的不等式bx2-ax-2>0的解集为( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com