Question

7．下列四种说法：
①函数y=$\frac{{x}^{2}-x+4}{x-1}$（x＞1）的最小值为5；
②等差数列{a_n}中，a₁，a₃，a₄成等比数列，则公比为$\frac{1}{2}$；
③已知a＞0，b＞0，a+b=1，则$\frac{2}{a}+\frac{3}{b}$的最小值为5+2$\sqrt{6}$；
④方程x²+ax+2b=0的两个实数根为x₁，x₂，且0＜x₁＜1＜x₂＜2，则$\frac{b-2}{a-1}$的取值范围是（$\frac{1}{4}$，1）．
其中正确的命题为①③④（填上所有正确命题的序号）．

Answer 1

分析 根据基本不等式，可判断①③；根据常数列也满足条件，可判断②；利用线性规划，可判断④

解答 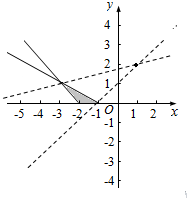解：当x＞1时，x-1＞0，
∴y=$\frac{{x}^{2}-x+4}{x-1}$=（x-1）+$\frac{4}{x-1}$+1≥2$\sqrt{（x-1）•\frac{4}{x-1}}$+1=5，故①正确；
等差数列{a_n}中，a₁，a₃，a₄成等比数列，
则a₃²=a₁•a₄，即（a₁+2d）²=a₁•（a₁+3d），
解得：a₁=-4d，或d=0，
则公比为$\frac{1}{2}$或1，
故②错误；
a＞0，b＞0，a+b=1，则$\frac{2}{a}+\frac{3}{b}$=（$\frac{2}{a}+\frac{3}{b}$）（a+b）=（$\frac{2b}{a}$+$\frac{3a}{b}$）+5≥5+2$\sqrt{6}$；
故③正确；
令f（x）=x²+ax+2b，若方程x²+ax+2b=0的两个实数根为x₁，x₂，且0＜x₁＜1＜x₂＜2，
则$\left\{\begin{array}{l}f（0）＞0\\ f（1）＜0\\ f（2）＞0\end{array}\right.$，即$\left\{\begin{array}{l}2b＞0\\ a+2b+1＜0\\ 2a+2b+4＞0\end{array}\right.$，
表示的平面区域Ω如图所示：

$\frac{b-2}{a-1}$表示平面区域Ω内一点（为包含边界）与（1，2）点连线的斜率，
故$\frac{b-2}{a-1}$的取值范围是（$\frac{1}{4}$，1）．
故④正确；
故答案为：①③④

点评 本题考查的知识点是基本不等式，线性规划，等差数列与等比数列，难度中档．