
【题目】已知函数f(x)=![]()
(1)求f(x)>0的解集;
(2)若x∈R时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)(0,+∞)(2)[![]() ,+∞)
,+∞)
【解析】
(1)通过对f(x)求导,可得x∈R时,f′(x)≥0,所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,x∈(0,+∞)时f(x)>0,不等式得解;
(2)若x∈R时,![]() 恒成立,不等式转化为2e
恒成立,不等式转化为2e![]() ex
ex![]() (x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e
(x∈R),因为都是偶函数,所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,构造新的函数F(x)=2e
e2x﹣1≥0成立即可,构造新的函数F(x)=2e![]() e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
e2x﹣1,求导后再对导函数进行分类讨论,可得实数m的取值范围.
(1)因为f(x)=![]() ,则f′(x)=
,则f′(x)=![]() ;
;
所以x∈R时,f′(x)≥0,
所以f(x)在(﹣∞,+∞)上单调递增,又f(0)=0,
所以x∈(﹣∞,0)时,f(x)<0,
x∈(0,+∞)时f(x)>0,
∴f(x)>0的解集为(0,+∞).
(2)因为x∈R时,2e![]() e2x+1恒成立,
e2x+1恒成立,
等价于![]() 恒成立,
恒成立,
即2e![]() ex
ex![]() (x∈R),
(x∈R),
因为都是偶函数,
所以只需x∈[0,+∞)时,2e![]() e2x﹣1≥0成立即可,
e2x﹣1≥0成立即可,
令F(x)=2e![]() e2x﹣1,F(0)=0,
e2x﹣1,F(0)=0,
F′(x)=2(2mx+1)e![]() 2e2x=2e2x[(2mx+1)e
2e2x=2e2x[(2mx+1)e![]() 1],F′(0)=0,
1],F′(0)=0,
令G(x)=(2mx+1)e![]() 1,G(0)=0,
1,G(0)=0,
G′(x)=2me![]() (2mx+1)(2mx﹣1)e
(2mx+1)(2mx﹣1)e![]() (4m2x2+2m﹣1)e
(4m2x2+2m﹣1)e![]()
①当2m﹣1≥0,即m![]() 时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
时,G′(x)≥0,所以G(x)在[0,+∞)上单调递增,
又因为G(0)=0,所以x∈[0,+∞)时,G(x)≥0,即F′(x)≥0,
所以F(x)在[0,+∞)上单调递增,又因为F(0)=0,所以x∈[0,+∞)时,F(x)≥0,所以m![]() 时满足要求;
时满足要求;
②当m=0,x=1时,2e<e2+1,不成立,所以m≠0;
③当2m﹣1<0且m≠0时,即m![]() 且m≠0时,x∈
且m≠0时,x∈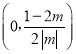 上单调递减,
上单调递减,
又因为G(0)=0,所以x∈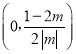 时,G(x)<0,即F′(x)<0,
时,G(x)<0,即F′(x)<0,
所以F(x)在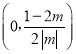 上单调递减,
上单调递减,
又因为F(0)=0,所以x∈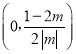 时,F(x)<0,
时,F(x)<0,
所以m![]() 且m≠0时不满足要求.
且m≠0时不满足要求.
综上所述,实数m的取值范围是[![]() ,+∞).
,+∞).


科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的方程为
的方程为![]() ,以极点为原点,极轴所在直线为
,以极点为原点,极轴所在直线为![]() 轴建立直角坐标,直线
轴建立直角坐标,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),
为参数),![]() 与
与![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ;若
;若![]() 、
、![]() 、
、![]() 成等比数列,求
成等比数列,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重100克,次品重110 克.现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品),如果将5袋产品以1-5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() =1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
=1,2,3,4,5),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() =__________克;若次品所在袋子的编号是
=__________克;若次品所在袋子的编号是![]() ,此时的重量
,此时的重量![]() =_________克.
=_________克.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A.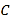 B.
B.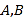
C.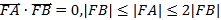 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,已知曲线
轴正半轴为极轴,建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com