
【题目】甲、乙两位同学进入新华书店购买数学课外阅读书籍,经过筛选后,他们都对![]() 三种书籍有购买意向,已知甲同学购买书籍
三种书籍有购买意向,已知甲同学购买书籍![]() 的概率分别为
的概率分别为![]() ,乙同学购买书籍
,乙同学购买书籍![]() 的概率分别为
的概率分别为![]() ,假设甲、乙是否购买
,假设甲、乙是否购买![]() 三种书籍相互独立.
三种书籍相互独立.
(1)求甲同学购买3种书籍的概率;
(2)设甲、乙同学购买2种书籍的人数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知圆![]() ,过点
,过点![]() 作直线
作直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(Ⅰ)当![]() 经过圆心
经过圆心![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(Ⅱ)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
(Ⅲ)求直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于四棱柱的说法:
①四条侧棱互相平行且相等;
②两对相对的侧面互相平行;
③侧棱必与底面垂直;
④侧面垂直于底面.
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣1+ ![]() (a∈R,e为自然对数的底数).
(a∈R,e为自然对数的底数).
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)求函数f(x)的极值;
(3)当a=1的值时,若直线l:y=kx﹣1与曲线y=f(x)没有公共点,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某数学兴趣小组为了研究人的脚的大小与身高的关系,随机抽测了20位同学,得到如下数据:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身高 | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
脚长 | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身高 | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
脚长 | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)请根据“序号为5的倍数”的几组数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成![]() 列联表,并根据列联表中数据说明能有多大的把握认为脚的大小与身高之间有关系.
列联表,并根据列联表中数据说明能有多大的把握认为脚的大小与身高之间有关系.
附表及公式: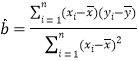 ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 列联表:
列联表:
高个 | 非高个 | 总计 | |
大脚 | |||
非大脚 | |||
总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在菱形ABCD中,∠A=60°,AB= ![]() ,将△ABC沿BD折起到△PBD的位置,若平面PBD⊥平面CBD,则三棱锥P﹣BCD的外接球体积为 .
,将△ABC沿BD折起到△PBD的位置,若平面PBD⊥平面CBD,则三棱锥P﹣BCD的外接球体积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com