
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S. ①当 ![]() 时,S为四边形
时,S为四边形
②截面在底面上投影面积恒为定值 ![]()
③不存在某个位置,使得截面S与平面A1BD垂直
④当 ![]() 时,S与C1D1的交点满足C1R1=
时,S与C1D1的交点满足C1R1= ![]()
其中正确命题的个数为 ( )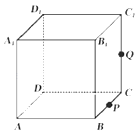
A.1
B.2
C.3
D.4
【答案】C
【解析】解:设截面与DD1相交于T,则AT∥PQ,且AT=2PQDT=2CQ. 对于①,当0<CQ< ![]() 时,则0<DT<1,所以截面S为四边形,且S为梯形,故①正确;
时,则0<DT<1,所以截面S为四边形,且S为梯形,故①正确;
对于②,当CQ> ![]() 时,投影面积不为
时,投影面积不为 ![]() ,故②不正确;
,故②不正确;
对于③,存在某个位置,使得截面S与平面A1BD垂直,故③正确;
对于④,当CQ= ![]() 时,如图,
时,如图,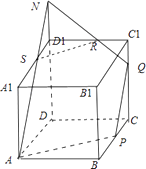
延长DD1至N,使D1N= ![]() ,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,可证AN∥PQ,由△NRD1∽△QRC1 , 可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=
,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,可证AN∥PQ,由△NRD1∽△QRC1 , 可得C1R:D1R=C1Q:D1N=1:2,故可得C1R= ![]() ,故④正确;
,故④正确;
故选:C.
【考点精析】关于本题考查的棱柱的结构特征,需要了解两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() (万元).当年产量不小于80千件时,C(x)=51x+
(万元).当年产量不小于80千件时,C(x)=51x+![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
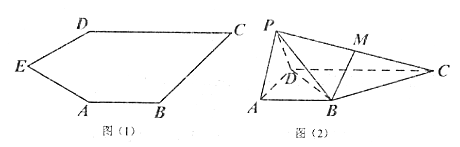
【题目】如图(1)五边形![]() 中,
中, ![]()
![]() ,将
,将![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() ,如图(2),点
,如图(2),点![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的体积为
的体积为![]() ,求四面体
,求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,g(x)=ax﹣3.
,g(x)=ax﹣3.
(1)当a=l时,确定函数h(x)=f(x)﹣g(x)在(0,+∞)上的单调性;
(2)若对任意x∈[0,4],总存在x0∈[﹣2,2],使得g(x0)=f(x)成立,求 实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)+g(x)=2x , 则有( )
A.f(3)<g(0)<f(4)
B.g(0)<f(4)<f(3)
C.g(0)<f(3)<f(4)
D.f(3)<f(4)<g(0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)已知满足![]() 的常数为
的常数为![]() .令函数
.令函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数, ![]() ),若
),若![]() 是
是![]() 的极值点,且
的极值点,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,集合A={x||x|≤2},B={x| ![]() >0},则A∩RB=( )
>0},则A∩RB=( )
A.[﹣2,1)
B.[﹣2,1]
C.[﹣2,2]
D.[﹣2,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com