
【题目】某地区对一种新品种小麦在一块试验田进行试种.从试验田中抽取![]() 株小麦,测量这些小麦的生长指标值,由测量结果得如下频数分布表:
株小麦,测量这些小麦的生长指标值,由测量结果得如下频数分布表:
生长指标值分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)求这![]() 株小麦生长指标值的样本平均数
株小麦生长指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)由直方图可以认为,这种小麦的生长指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() .
.
①利用该正态分布,求![]() ;
;
②若从试验田中抽取![]() 株小麦,记
株小麦,记![]() 表示这
表示这![]() 株小麦中生长指标值位于区间
株小麦中生长指标值位于区间![]() 的小麦株数,利用①的结果,求
的小麦株数,利用①的结果,求![]() .
.
附: ![]() .
.
若![]() ,则
,则![]() ,
,
![]() .
.
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相较于点
相较于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立直角坐标系.
轴的正半轴为极轴建立直角坐标系.
(1)求曲线![]() 的极坐标方程,直线
的极坐标方程,直线![]() 的普通方程;
的普通方程;
(2)把直线![]() 向左平移一个单位得到直线
向左平移一个单位得到直线![]() ,设
,设![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,
, ![]() ,
, ![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是____.
不重合),则下列结论正确的是____.
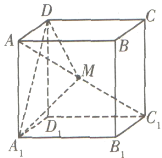
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面积不可能等于
的面积不可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=-![]() .
.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,F关于原点的对称点为P,过F作
的焦点为F,F关于原点的对称点为P,过F作![]() 轴的垂线交抛物线于M,N两点,给出下列三个结论:
轴的垂线交抛物线于M,N两点,给出下列三个结论:
①![]() 必为直角三角形;
必为直角三角形;
②直线![]() 必与抛物线相切;
必与抛物线相切;
③![]() 的面积为
的面积为![]() .其中正确的结论是___.
.其中正确的结论是___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 在抛物线
在抛物线![]() 外,过点
外,过点![]() 作抛物线
作抛物线![]() 的两切线,设两切点分别为
的两切线,设两切点分别为![]() ,
,![]() ,记线段
,记线段![]() 的中点为
的中点为![]() .
.

(Ⅰ)求切线![]() ,
,![]() 的方程;
的方程;
(Ⅱ)证明:线段![]() 的中点
的中点![]() 在抛物线
在抛物线![]() 上;
上;
(Ⅲ)设点![]() 为圆
为圆![]() 上的点,当
上的点,当![]() 取最大值时,求点
取最大值时,求点![]() 的纵坐标.
的纵坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间(a,b),[a,b),(a,b],[a,b]的长度均为![]() ,多个区间并集的长度为各区间长度之和,例如,(1,2)
,多个区间并集的长度为各区间长度之和,例如,(1,2) ![]() [3,5)的长度d=(2-1)+(5-3)=3. 用[x]表示不超过x的最大整数,记{x}=x-[x],其中
[3,5)的长度d=(2-1)+(5-3)=3. 用[x]表示不超过x的最大整数,记{x}=x-[x],其中![]() .设
.设![]() ,
, ![]() ,当
,当![]() 时,不等式
时,不等式![]() 解集区间的长度为
解集区间的长度为![]() ,则
,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com