
【题目】△ABC的外接圆半径R= ![]() ,角A,B,C的对边分别是a,b,c,且
,角A,B,C的对边分别是a,b,c,且 ![]() =
= ![]()
(1)求角B和边长b;
(2)求S△ABC的最大值及取得最大值时的a,c的值,并判断此时三角形的形状.
【答案】
(1)解:∵ ![]() ,
,
∴2sinAcosB﹣sinCcosB=sinBcosC,可得2sinAcosB=sinBcosC+cosBsinC=sin(B+C),
∵在△ABC中,sin(B+C)=sin(π﹣A)=sinA>0,
∴2sinAcosB=sinA,可得cosB= ![]() .
.
又∵B∈(0,π),∴ ![]() ,
,
由正弦定理 ![]() ,可得b=2RsinB=2
,可得b=2RsinB=2 ![]() sin
sin ![]() =3
=3
(2)解:∵b=3, ![]() ,
,
∴由余弦定理b2=a2+c2﹣2accosB,得a2+c2﹣ac=9,
因此,ac+9=a2+c2≥2ac,可得ac≤9,当且仅当a=c时等号成立,
∵S△ABC= ![]() =
= ![]() ,∴
,∴ ![]()
由此可得:当且仅当a=c时,S△ABC有最大值 ![]() ,此时a=b=c=3,可得△ABC是等边三角形
,此时a=b=c=3,可得△ABC是等边三角形
【解析】(1)运用两角和的正弦公式将已知等式化简整理,得到2sinAcosB=sin(B+C),根据三角函数的诱导公式可得sin(B+C)=sinA>0,从而得出cosB= ![]() ,可得
,可得 ![]() ,最后由正弦定理加以计算,可得边b的长;(2)由b=3且
,最后由正弦定理加以计算,可得边b的长;(2)由b=3且 ![]() ,利用余弦定理算出a2+c2﹣ac=9,再根据基本不等式算出ac≤9.利用三角形的面积公式算出S△ABC=
,利用余弦定理算出a2+c2﹣ac=9,再根据基本不等式算出ac≤9.利用三角形的面积公式算出S△ABC= ![]() ,从而得到当且仅当a=c时,S△ABC有最大值
,从而得到当且仅当a=c时,S△ABC有最大值 ![]() ,进而得到此时△ABC是等边三角形.
,进而得到此时△ABC是等边三角形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax3+bx2+cx+d(a、b、c、d∈R)满足:x∈R都有f(x)+f(﹣x)=0,且x=1时,f(x)取极小值![]() .
.
(1)f(x)的解析式;
(2)当x∈[﹣1,1]时,证明:函数图象上任意两点处的切线不可能互相垂直:
(3)设F(x)=|xf(x)|,证明: ![]() 时,
时, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队参加听歌猜歌名游戏,每队3人.随机播放一首歌曲,参赛者开始抢答,每人只有一次抢答机会(每人抢答机会均等),答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(Ⅰ)若比赛前随机从两队的6个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
(Ⅱ)用ξ表示甲队的总得分,求随机变量ξ的分布列和数学期望;
(Ⅲ)求两队得分之和大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足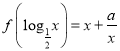 为常数
为常数
(1)求函数f(x)的表达式;
(2)如果f(x)为偶函数,求a的值;
(3)当f(x)为偶函数时,若方程f(x)=m有两个实数根x1,x2;其中x1<0,0<x2<1;求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下三个命题 ①设回归方程为 ![]() =3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
=3﹣3x,则变量x增加一个单位时,y平均增加3个单位;
②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N (1,σ2) (σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|).
(1)求实数a,b的值;
(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com