
【题目】用红、黄、蓝三种不同颜色给图中的![]() 个矩形随机涂色,每个矩形只涂一种颜色,则
个矩形随机涂色,每个矩形只涂一种颜色,则![]() 个矩形颜色都相同的概率是________,
个矩形颜色都相同的概率是________,![]() 个矩形颜色都不同的概率是________.
个矩形颜色都不同的概率是________.

【答案】![]()
![]()
【解析】
列举出所有的基本事件以及事件“![]() 个矩形颜色都相同”和事件“
个矩形颜色都相同”和事件“![]() 个矩形颜色都不同”所包含的基本事件,利用古典概型的概率公式可计算出所求事件的概率.
个矩形颜色都不同”所包含的基本事件,利用古典概型的概率公式可计算出所求事件的概率.
以“红黄蓝”表示从左到右三个矩形所涂的颜色,则所有的基本事件有:红红红、红红黄、红红蓝、红黄红、红黄黄、红黄蓝、红蓝红、红蓝黄、红蓝蓝、黄红红、黄红黄、黄红蓝、黄黄红、黄黄黄、黄黄蓝、黄蓝红、黄蓝黄、黄蓝蓝、蓝红红、蓝红黄、蓝红蓝、蓝黄红、蓝黄黄、蓝黄蓝、蓝蓝红、蓝蓝黄、蓝蓝蓝,共![]() 个基本事件,
个基本事件,
事件“![]() 个矩形颜色都相同”所包含的基本事件有:红红红、黄黄黄、蓝蓝蓝,共
个矩形颜色都相同”所包含的基本事件有:红红红、黄黄黄、蓝蓝蓝,共![]() 个基本事件,所以,
个基本事件,所以,![]() 个矩形颜色都相同的概率是
个矩形颜色都相同的概率是![]() .
.
事件“![]() 个矩形颜色都不同”所包含的基本事件有:红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝黄红、蓝红黄,共
个矩形颜色都不同”所包含的基本事件有:红黄蓝、红蓝黄、黄红蓝、黄蓝红、蓝黄红、蓝红黄,共![]() 个基本事件,所以,
个基本事件,所以,![]() 个矩形颜色都不同的概率是
个矩形颜色都不同的概率是![]() .
.
故答案为:![]() ;
;![]() .
.


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
【题目】某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖励金额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.现有三个奖励模型:![]() ,
,![]() ,
,![]() ,其中哪个模型能符合公司的要求?
,其中哪个模型能符合公司的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入![]() 世纪以来,该产品的产量平稳增长.记
世纪以来,该产品的产量平稳增长.记![]() 年为第
年为第![]() 年,且前
年,且前![]() 年中,第
年中,第![]() 年与年产量
年与年产量![]() 万件之间的关系如下表所示:
万件之间的关系如下表所示:
|
|
|
|
|
|
|
|
|
|
若![]() 近似符合以下三种函数模型之一:
近似符合以下三种函数模型之一:![]() ,
,![]() ,
,![]() .
.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,![]() 年的年产量比预计减少
年的年产量比预计减少![]() ,试根据所建立的函数模型,确定
,试根据所建立的函数模型,确定![]() 年的年产量.
年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】因客流量临时增大,某鞋店拟用一个高为50![]() (即
(即![]() )的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客
)的平面镜自制一个竖直摆放的简易鞋镜,根据经验:一般顾客![]() 的眼睛
的眼睛![]() 到地面的距离为
到地面的距离为![]() (
(![]() )在区间
)在区间![]() 内,设支架
内,设支架![]() 高为
高为![]() (
(![]() )
)![]() ,
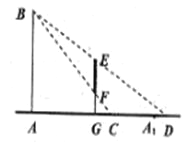
,![]() ,顾客可视的镜像范围为
,顾客可视的镜像范围为![]() (如图所示),记
(如图所示),记![]() 的长度为
的长度为![]() (
(![]() ).
).
(I)当![]() 时,试求
时,试求![]() 关于
关于![]() 的函数关系式和
的函数关系式和![]() 的最大值;
的最大值;
(II)当顾客的鞋![]() 在镜中的像
在镜中的像![]() 满足不等关系
满足不等关系![]() (不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求
(不计鞋长)时,称顾客可在镜中看到自己的鞋,若使一般顾客都能在镜中看到自己的鞋,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费![]() 和年销售量
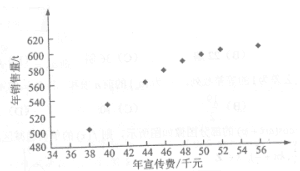
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() =
=![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,![]() 与
与![]() ,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利z与x,y的关系为![]() ,根据(Ⅱ)的结果回答下列问题:
,根据(Ⅱ)的结果回答下列问题:
(Ⅰ)当年宣传费![]() 时,年销售量及年利润的预报值时多少?
时,年销售量及年利润的预报值时多少?
(Ⅱ)当年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
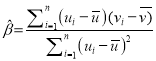 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,求n≥m+2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com