
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为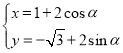 (其中
(其中![]() 为参数,
为参数,![]() ).在极坐标系(以坐标原点
).在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上恰有一个点到曲线
上恰有一个点到曲线![]() 的距离为1,求曲线
的距离为1,求曲线![]() 的直角坐标方程.
的直角坐标方程.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,数列{an}满足a1=a,an+1=an﹣(an﹣2)3,则( )
A.当a=4时,a10>210B.当![]() 时,a10>2
时,a10>2
C.当![]() 时,a10>210D.当
时,a10>210D.当![]() 时,a10>2
时,a10>2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
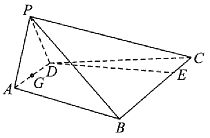
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某高校综合评价有两步:第一步是材料初审,若材料初审不合格,则不能进入第二步面试;若材料初审合格,则进入第二步面试.只有面试合格者,才能获得该高校综合评价的录取资格,现有A,B,C三名学生报名参加该高校的综合评价,假设A,B,C三位学生材料初审合格的概率分别是![]() ,
,![]() ,
,![]() ;面试合格的概率分别是
;面试合格的概率分别是![]() ,
,![]() ,
,![]() .
.
(1)求A,B两位考生有且只有一位考生获得录取资格的概率;
(2)记随机变量X为A,B,C三位学生获得该高校综合评价录取资格的人数,求X的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区为了了解业主用水情况,该小区分为一期和二期,入住共达4000户,现在通过随机抽样获得了100户居民的月均用水量,下图是调查结果的频数分布表和频率分布直方图.
分组 |
|
|
|
|
|
频数 | 4 | 8 | 15 | 22 | 25 |
分组 |
|
|
|
| |
频数 | 14 | 6 | 4 | 2 |
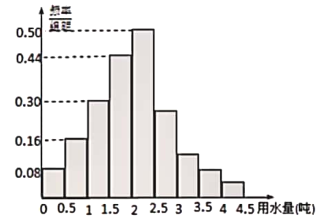
(1)估计该小区月均用水量超过3.8吨约有多少户;(2)通过频率分布直方图,估计该小区居民月均用水量平均值和中位数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小芳、小明两人各拿两颗质地均匀的骰子做游戏,规则如下:若掷出的点数之和为4的倍数,则由原投掷人继续投掷;若掷出的点数之和不是4的倍数,则由对方接着投掷.
(1)规定第1次从小明开始.
(ⅰ)求前4次投掷中小明恰好投掷2次的概率;
(ⅱ)设游戏的前4次中,小芳投掷的次数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
(2)若第1次从小芳开始,求第![]() 次由小芳投掷的概率
次由小芳投掷的概率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com