
已知正整数![]() 满足条件:对于任意正整数n,从集合
满足条件:对于任意正整数n,从集合![]() 中不重复地任取
中不重复地任取
若干个数,这些数之间经过加减运算后所得的数的绝对值为互不相同的正整数,且这些
正整数与![]() 一起恰好是1至Sn全体自然数组成的集合,其中Sn为数列
一起恰好是1至Sn全体自然数组成的集合,其中Sn为数列![]() 的前n项和。
的前n项和。
(1)求a1,a2的值;(2)求数列![]() 的通项公式。
的通项公式。
科目:高中数学 来源: 题型:
| 1 |
| an•an+1 |
| m |
| 23 |
查看答案和解析>>
科目:高中数学 来源:江西省新余一中2010届高三第六次模拟考试数学理科试题 题型:044
已知sin(2α+β)=3sinβ,设tanα=x,tanβ=y,记y=f(x).
(1)求f(x)的表达式;
(2)定义正数数列{an}:a1=![]() ,
,![]() =2an·f(an)(n∈N*).试求数列{an}的通项公式;
=2an·f(an)(n∈N*).试求数列{an}的通项公式;
(3)在(2)的条件下,记bn=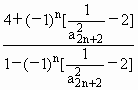 ,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年大连市双基测试文)(14分)已知等差数列{an}满足![]() ,设Sn是数列
,设Sn是数列![]() 的前n项和,
的前n项和,
记![]()
(1)求![]() ;
;
(2) 比较![]() 与
与![]() 其中
其中![]() 的大小;
的大小;
(3)如果函数![]() 对一切大于1的正整数n其函数值都小于零,那么a、b应满足什么条件.
对一切大于1的正整数n其函数值都小于零,那么a、b应满足什么条件.
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省高一下学期期中考试数学试卷 题型:解答题
.已知正项数列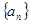 的首项
的首项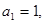 前
前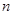 项和为
项和为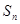 ,且满足
,且满足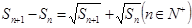 .
.
(Ⅰ)求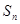 与
与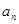
(Ⅱ)从集合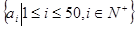 取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M.
取出三个数构成以正整数为公比的递增等比数列,放回后再取出三个数构成以正整数为公比的递增等比数列,相同的数列只取一次,按照上述取法取下去,直到取完所有满足条件的数列为止。求满足上述条件的所有的不同数列的和M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com