A
分析:由题设条件,可分两步研究本题,先探究m=1时直线mx+y+1=0和直线x-my+3=0互相垂直是否成立,再探究直线mx+y+1=0和直线x-my+3=0互相垂直时m的可能取值,再依据充分条件必要条件做出判断,得出答案
解答:当m=1时,两直线的方程分别为x+y+1=0,与x-y+3=0,可得出此两直线是垂直的
当两直线垂直时,
①当m=0时,符合题意,
②当m≠0时,两直线的斜率分别是-m与

,由两直线垂直得
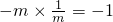
得m∈R且m≠0
由上知,“m=1”可得出直线mx+y+1=0和直线x-my+3=0垂直;
由直线mx+y+1=0和直线x-my+3=0垂直”可得出m∈R
所以m=1是直线mx+y+1=0和直线x-my+3=0垂直的充分不必要条件
故选A.
点评:本题考查充分条件必要条件的判断及两直线垂直的条件,解题的关键是理解充分条件与必要条件的定义及两直线垂直的条件,本题的难点是由两直线垂直得出参数m的取值,此处也是一易错点,易忘记验证斜率不存在的情况,导致判断失误.

 ,由两直线垂直得
,由两直线垂直得 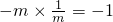 得m∈R且m≠0
得m∈R且m≠0
