
【题目】已知椭圆E:![]() (a>b>0)的离心率e
(a>b>0)的离心率e![]() .
.
(1)若点P(1,![]() )在椭圆E上,求椭圆E的标准方程;
)在椭圆E上,求椭圆E的标准方程;
(2)若D(2,0)在椭圆内部,过点D斜率为![]() 的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
的直线交椭圆E于M.N两点,|MD|=2|ND|,求椭圆E的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)因为![]() ,所以
,所以![]() ,则
,则![]() ,所以
,所以![]() ,将P(1,
,将P(1,![]() )代入方程,得b2=1,所以a2=4,可得椭圆方程;
)代入方程,得b2=1,所以a2=4,可得椭圆方程;
(2)设M(x1,y1),N(x2,y2),设y1<y2,因为![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() ,MN的直线方程为x
,MN的直线方程为x![]() 2,联立求解韦达定理,结合条件|MD|=2|ND|,可得y1=﹣2y2,所以解得
2,联立求解韦达定理,结合条件|MD|=2|ND|,可得y1=﹣2y2,所以解得![]() ,
,![]() ,代入根与系数关系,得b2=3,a2=12,求得椭圆E的方程.
,代入根与系数关系,得b2=3,a2=12,求得椭圆E的方程.
(1)因为![]() ,所以
,所以![]() ,则
,则![]() ,所以
,所以![]() ,
,
将P(1,![]() )代入方程,得b2=1,所以a2=4,
)代入方程,得b2=1,所以a2=4,
所以椭圆E的标准方程为![]() ;
;
(2)设M(x1,y1),N(x2,y2),不妨设y1<y2,
因为![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() ,MN的直线方程为x
,MN的直线方程为x![]() 2,
2,
联立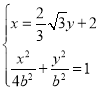 ,得,16y2+8
,得,16y2+8![]() y+12﹣12b2=0,
y+12﹣12b2=0,
所以y1+y2![]() ,y1y2
,y1y2![]() ①.
①.
因为|MD|=2|ND|,即y1=﹣2y2,所以![]() ,
,![]() ,
,
代入①,得b2=3,a2=12,
所以椭圆E的方程为![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
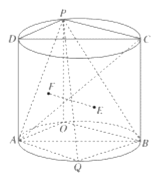
【题目】如图,圆柱的轴截面![]() 是边长为2的正方形,点P是圆弧
是边长为2的正方形,点P是圆弧![]() 上的一动点(不与
上的一动点(不与![]() 重合),点Q是圆弧
重合),点Q是圆弧![]() 的中点,且点
的中点,且点![]() 在平面
在平面![]() 的两侧.
的两侧.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)设点P在平面![]() 上的射影为点O,点
上的射影为点O,点![]() 分别是
分别是![]() 和
和![]() 的重心,当三棱锥
的重心,当三棱锥![]() 体积最大时,回答下列问题.
体积最大时,回答下列问题.
(i)证明:![]() 平面
平面![]() ;
;
(ii)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.命题“p且q”为真,则![]() 恰有一个为真命题
恰有一个为真命题
B.命题“已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件”
”的充分不必要条件”
C.命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]()
D.如果函数![]() 在区间
在区间![]() 上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有![]() ,那么函数
,那么函数![]() 在区间
在区间![]() 内有零点
内有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意x∈R,存在函数f(x)满足( )
A.f(cosx)=sin2xB.f(sin2x)=sinx
C.f(sinx)=sin2xD.f(sinx)=cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)如果函数![]() 在公共定义域D上,满足
在公共定义域D上,满足![]() ,那么就称
,那么就称![]() 为
为![]() 的“伴随函数”.已知函数
的“伴随函数”.已知函数![]() ,
,![]() .若在区间
.若在区间![]() 上,函数
上,函数![]() 是
是![]() 的“伴随函数”,求实数
的“伴随函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,正实数
,正实数![]() 满足
满足![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com