(本小题12分)已知函数
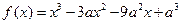
.
(1) 设
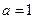
,求函数
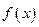
的极值;
(2)若
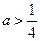
,且当
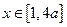
时,
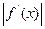
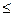
12a恒成立,试确定
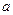
的取值范围.
解:(Ⅰ)当a=1时,对函数
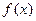
求导数,得
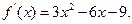
…2分
令
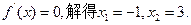
列表讨论
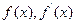
的变化情况:
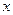
| 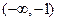
| 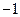
| (-1,3)
| 3
| 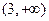
|
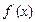
| +
| 0
| —
| 0
| +
|
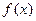
| 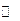
| 极大值6
| 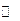
| 极小值-26
| 
|
所以,
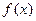
的极大值是

,极小值是
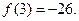
………………6分
(Ⅱ)
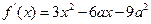
的图像是一条开口向上的抛物线,关于x=a对称.
若
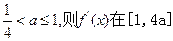
上是增函数,从而
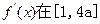
上的最小值是
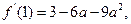
最大值是
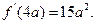
由
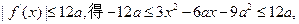
于是有 …………8分
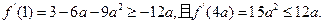
由
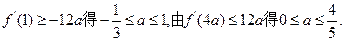
………10分
所以

若a>1,则
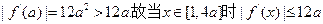
不恒成立.
所以使
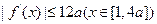
恒成立的a的取值范围是
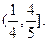
………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(12分)已知函数f(x)=
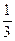
ax
3-bx
2 +(2-b)x+1,在x=x
2处取得极大值,在x=x
2处取得极小值,且0<x
1<1<x
2<2。
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
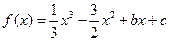
,且
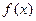
在
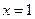
处取得极值.
(1)求
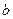
的值;
(2)若当
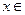
[-1,
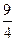
]时,
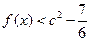
恒成立,求
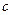
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知函数
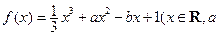
,
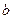
为实数)有极值,且在
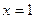
处的切线与直线
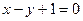
平行.
(1)求实数
a的取值范围;
(2)是否存在实数
a,使得函数
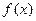
的极小值为1,若存在,求出实数
a的值;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数f(x)=
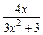
,x∈[0,2].
(1)求f(x)的值域;
(2)设a≠0,函数g(x)=
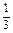
ax
3-a
2x,x∈[0,2].若对任意x
1∈[0,2],总存在x
2∈[0,2],使f(x
1)-g(x
2)=0.求实数a的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(12分)设函数
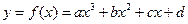
的图象与y轴交点为p,且曲线在p点处的切线方程为
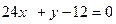
.若函数在
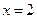
处取得极值-16,求函数解析式.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设
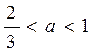
,函数
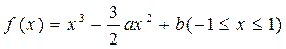
的最大值为1,最小值为
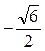
,则常数
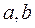
的值分别为
和
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
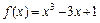
在区间[
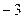
,0]上的最小值是
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在
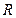
上可导的函数
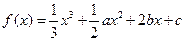
,当
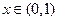
时取得极大值,当
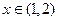
时取得极小值,则
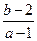
的取值范围是 ( )
查看答案和解析>>

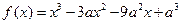 .
.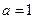 ,求函数
,求函数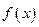 的极值;
的极值;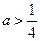 ,且当
,且当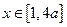 时,
时,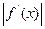
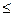 12a恒成立,试确定
12a恒成立,试确定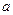 的取值范围.
的取值范围.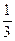 ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。
ax3-bx2 +(2-b)x+1,在x=x2处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2。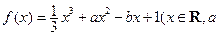 ,
,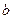 为实数)有极值,且在
为实数)有极值,且在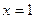 处的切线与直线
处的切线与直线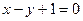 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;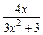 ,x∈[0,2].
,x∈[0,2].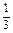 ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.
ax3-a2x,x∈[0,2].若对任意x1∈[0,2],总存在x2∈[0,2],使f(x1)-g(x2)=0.求实数a的取值范围.