
ЁОЬтФПЁПФГВтЪдЭХЖгЮЊСЫбаОПЁАвћОЦЁБЖдЁАМнГЕАВШЋЁБЕФгАЯьЃЌЫцЛњбЁШЁ![]() УћМнЪЛдБЯШКѓдкЮоОЦзДЬЌЁЂОЦКѓзДЬЌЯТНјааЁАЭЃГЕОрРыЁБВтЪдЃЌВтЪдЕФЗНАИЃКЕчФдФЃФтМнЪЛЃЌвдФГЫйЖШдШЫйааЪЛЃЌМЧТМЯТМнЪЛдБЕФЁАЭЃГЕОрРыЁБЃЈМнЪЛдБДгПДЕНвтЭтЧщПіЕНГЕзгЭЃЯТЫљашвЊЕФОрРыЃЉЃЌЮоОЦзДЬЌгыОЦКѓзДЬЌЯТЕФЪдбщЪ§ОнЗжБ№СагкБэ
УћМнЪЛдБЯШКѓдкЮоОЦзДЬЌЁЂОЦКѓзДЬЌЯТНјааЁАЭЃГЕОрРыЁБВтЪдЃЌВтЪдЕФЗНАИЃКЕчФдФЃФтМнЪЛЃЌвдФГЫйЖШдШЫйааЪЛЃЌМЧТМЯТМнЪЛдБЕФЁАЭЃГЕОрРыЁБЃЈМнЪЛдБДгПДЕНвтЭтЧщПіЕНГЕзгЭЃЯТЫљашвЊЕФОрРыЃЉЃЌЮоОЦзДЬЌгыОЦКѓзДЬЌЯТЕФЪдбщЪ§ОнЗжБ№СагкБэ![]()
ЭЃГЕОрРы |
|
|
|
|
|
ЦЕЪ§ | 26 |
|
| 8 | 2 |
Бэ![]()
ЦНОљУПКСЩ§бЊвКОЦОЋКЌСП | 10 | 30 | 50 | 70 | 90 | /tr>
ЦНОљЭЃГЕОрРы | 30 | 50 | 60 | 70 | 90 |
вбжЊБэ![]() Ъ§ОнЕФжаЮЛЪ§ЙРМЦжЕЮЊ
Ъ§ОнЕФжаЮЛЪ§ЙРМЦжЕЮЊ![]() ЃЌЛиД№вдЯТЮЪЬт.
ЃЌЛиД№вдЯТЮЪЬт.
(Ђё)Чѓ![]() ЕФжЕЃЌВЂЙРМЦМнЪЛдБЮоОЦзДЬЌЯТЭЃГЕОрРыЕФЦНОљЪ§ЃЛ
ЕФжЕЃЌВЂЙРМЦМнЪЛдБЮоОЦзДЬЌЯТЭЃГЕОрРыЕФЦНОљЪ§ЃЛ
ЃЈЂђЃЉИљОнзюаЁЖўГЫЗЈЃЌгЩБэ![]() ЕФЪ§ОнМЦЫу
ЕФЪ§ОнМЦЫу![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬ
ЕФЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈЂѓЃЉИУВтЪдЭХЖгШЯЮЊЃКМнЪЛдБОЦКѓМнГЕЕФЦНОљЁАЭЃГЕОрРыЁБ![]() ДѓгкЃЈЂёЃЉжаЮоОЦзДЬЌЯТЕФЭЃГЕОрРыЦНОљЪ§ЕФ
ДѓгкЃЈЂёЃЉжаЮоОЦзДЬЌЯТЕФЭЃГЕОрРыЦНОљЪ§ЕФ![]() БЖЃЌдђШЯЖЈМнЪЛдБЪЧЁАзэМнЁБ.ЧыИљОн(Ђђ)жаЕФЛиЙщЗНГЬ,дЄВтЕБУПКСЩ§бЊвКОЦОЋКЌСПДѓгкЖрЩйКСПЫЪБЮЊЁАзэМнЁБЃП
БЖЃЌдђШЯЖЈМнЪЛдБЪЧЁАзэМнЁБ.ЧыИљОн(Ђђ)жаЕФЛиЙщЗНГЬ,дЄВтЕБУПКСЩ§бЊвКОЦОЋКЌСПДѓгкЖрЩйКСПЫЪБЮЊЁАзэМнЁБЃП
ЃЈИНЃКЛиЙщЗНГЬ![]() жаЃЌ
жаЃЌ 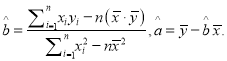 ЃЉ
ЃЉ
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЛЃЈЂђЃЉ
ЃЛЃЈЂђЃЉ ![]() ЃЛЃЈЂѓЃЉШЯЖЈЮЊЁАзэМнЁБ.
ЃЛЃЈЂѓЃЉШЯЖЈЮЊЁАзэМнЁБ.
ЁОНтЮіЁПЪдЬтЗжЮіЃК(ЂёЃЉИљОнБэ1МАжаЮЛЪ§ЕФИХФюПЩЧѓГі![]() ЃЛЃЈЂђЃЉгЩЛиЙщЯЕЪ§ЙЋЪНЧѓГі
ЃЛЃЈЂђЃЉгЩЛиЙщЯЕЪ§ЙЋЪНЧѓГі![]() МДПЩЃЛЃЈЂѓЃЉгЩЃЈЂёЃЉжЊЕБ
МДПЩЃЛЃЈЂѓЃЉгЩЃЈЂёЃЉжЊЕБ![]() ЪБШЯЖЈМнЪЛдБЪЧЁАзэМнЁБЃЌСю
ЪБШЯЖЈМнЪЛдБЪЧЁАзэМнЁБЃЌСю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌЕБУПКСЩ§бЊвКОЦОЋКЌСПДѓгк
ЃЌЕБУПКСЩ§бЊвКОЦОЋКЌСПДѓгк![]() КСПЫЪБШЯЖЈЮЊЁАзэМнЁБЃЎ
КСПЫЪБШЯЖЈЮЊЁАзэМнЁБЃЎ
ЪдЬтНтЮіЃКЃЈЂёЃЉвРЬтвтЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
гж![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЙЪЭЃГЕОрРыЕФЦНОљЪ§ЮЊ![]()
ЃЈЂђЃЉвРЬтвтЃЌПЩжЊ![]() ЃЌ
ЃЌ
![]()
![]() ,
,
![]() ,
,
ЫљвдЛиЙщжБЯпЮЊ![]()
ЃЈЂѓЃЉгЩЃЈЂёЃЉжЊЕБ![]() ЪБШЯЖЈМнЪЛдБЪЧЁАзэМнЁБ
ЪБШЯЖЈМнЪЛдБЪЧЁАзэМнЁБ
Сю![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ,
,
ЕБУПКСЩ§бЊвКОЦОЋКЌСПДѓгк![]() КСПЫЪБШЯЖЈЮЊЁАзэМнЁБЃЎ
КСПЫЪБШЯЖЈЮЊЁАзэМнЁБЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкаБШ§Ртжљ![]() жаЃЌ
жаЃЌ![]() ЃЌЦНУц
ЃЌЦНУц![]() ЕзУц
ЕзУц![]() ЃЌЕу
ЃЌЕу![]() ЁЂDЗжБ№ЪЧЯпЖЮ
ЁЂDЗжБ№ЪЧЯпЖЮ![]() ЁЂBCЕФжаЕуЃЎ
ЁЂBCЕФжаЕуЃЎ

ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃКAD//ЦНУц![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌе§ШЗЕФУќЬтга__________ЃЎ
ЂйЛиЙщжБЯп![]() КуЙ§бљБОЕуЕФжааФ
КуЙ§бљБОЕуЕФжааФ![]() ЃЌЧвжСЩйЙ§вЛИібљБОЕуЃЛ
ЃЌЧвжСЩйЙ§вЛИібљБОЕуЃЛ
ЂкНЋвЛзщЪ§ОнЕФУПИіЪ§ОнЖММгвЛИіЯрЭЌЕФГЃЪ§КѓЃЌЗНВюВЛБфЃЛ
ЂлгУЯрЙижИЪ§![]() РДПЬЛЛиЙщаЇЙћЃЌ
РДПЬЛЛиЙщаЇЙћЃЌ ![]() дННгНќ
дННгНќ![]() ЃЌЫЕУїФЃаЭЕФФтКЯаЇЙћдНКУЃЛ
ЃЌЫЕУїФЃаЭЕФФтКЯаЇЙћдНКУЃЛ
ЂмгУЯЕЭГГщбљЗЈДг![]() УћбЇЩњжаГщШЁШнСПЮЊ
УћбЇЩњжаГщШЁШнСПЮЊ![]() ЕФбљБОЃЌНЋ
ЕФбљБОЃЌНЋ![]() УћбЇЩњДг
УћбЇЩњДг![]() БрКХЃЌАДБрКХЫГађЦНОљЗжГЩ
БрКХЃЌАДБрКХЫГађЦНОљЗжГЩ![]() зщЃЈ
зщЃЈ![]() КХЃЌ
КХЃЌ ![]() КХЃЌ
КХЃЌ ![]() КХЃЉЃЌШєЕк
КХЃЉЃЌШєЕк![]() зщГщГіЕФКХТыЮЊ
зщГщГіЕФКХТыЮЊ![]() ЃЌдђЕквЛзщжагУГщЧЉЗЈШЗЖЈЕФКХТыЮЊ
ЃЌдђЕквЛзщжагУГщЧЉЗЈШЗЖЈЕФКХТыЮЊ![]() КХ.
КХ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=2x2+bx+cдк ![]() ЩЯЪЧМѕКЏЪ§ЃЌдк
ЩЯЪЧМѕКЏЪ§ЃЌдк ![]() ЩЯЪЧдіКЏЪ§ЃЌЧвСНИіСуЕуx1 ЃЌ x2Тњзу|x1Љx2|=2ЃЌЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЎ
ЩЯЪЧдіКЏЪ§ЃЌЧвСНИіСуЕуx1 ЃЌ x2Тњзу|x1Љx2|=2ЃЌЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=alnЃЈx+1ЃЉЉx2 ЃЌ дкЃЈ1ЃЌ2ЃЉФкШЮШЁСНИіЪЕЪ§x1 ЃЌ x2ЃЈx1Ёйx2ЃЉЃЌШєВЛЕШЪН ![]() ЃО1КуГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
ЃО1КуГЩСЂЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЮЊЃЈ ЃЉ
A.ЃЈ28ЃЌ+ЁоЃЉ
B.[15ЃЌ+ЁоЃЉ
C.[28ЃЌ+ЁоЃЉ
D.ЃЈ15ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЪЧЦцКЏЪ§ЃЌЕБxЃО0ЪБЃЌfЃЈxЃЉ=axЃЈxЃО0ЧвaЁй1ЃЉЃЌЧвfЃЈlog ![]() 4ЃЉ=Љ3ЃЌдђaЕФжЕЮЊЃЈ ЃЉ
4ЃЉ=Љ3ЃЌдђaЕФжЕЮЊЃЈ ЃЉ
A.![]()
B.3
C.9
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЈ
ЃЈ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ
ЃЈЂёЃЉЪдЬжТлКЏЪ§![]() ЕФСуЕуИіЪ§ЃЛ
ЕФСуЕуИіЪ§ЃЛ
ЃЈЂђЃЉжЄУїЃКЕБ![]() Чв
Чв![]() ЪБЃЌзмга
ЪБЃЌзмга![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ.
ЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉ.
ЃЈ1ЃЉЪдЬжТлКЏЪ§![]() ЕФМЋжЕЧщПіЃЛ
ЕФМЋжЕЧщПіЃЛ
ЃЈ2ЃЉжЄУїЃКЕБ![]() Чв
Чв![]() ЪБЃЌзмга
ЪБЃЌзмга![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊfЃЈxЃЉ=m2x+x2+nxЃЌШє{x|fЃЈxЃЉ=0}={x|fЃЈfЃЈxЃЉЃЉ=0}ЁйЃЌдђm+nЕФШЁжЕЗЖЮЇЮЊ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com