
【题目】已知幂函数f(x)的图象经过点 ![]() . (Ⅰ)求函数f(x)的解析式;
. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)判断函数f(x)在区间(0,+∞)上的单调性,并用单调性的定义证明.
【答案】解:(Ⅰ)∵f(x)是幂函数,则设f(x)=xα(α是常数), ∵f(x)的图象过点 ![]() ,
,
∴ ![]() ,
,
∴α=﹣23,
故f(x)=x﹣2 , 即 ![]() ;
;
(Ⅱ)f(x)在区间(0,+∞)上是减函数.证明如下:
设x1 , x2∈(0,+∞),且x1<x2 ,
∴ ![]() ,
,
∵0<x1<x2∈(0,+∞),
∴x2﹣x1>0, ![]() ,
,
∴f(x1)﹣f(x2)>0,即f(x1)>f(x2),
∴f(x)在区间(0,+∞)上是减函数
【解析】(Ⅰ)利用幂函数的定义,设f(x)=xα(α是常数),根据f(x)的图象过点 ![]() ,列出关于α的方程,求解即可得到答案;(Ⅱ)设x1 , x2∈(0,+∞),且x1<x2 , 作差f(x1)﹣f(x2)化简到能直接判断符号为止,利用函数单调性的定义,即可证得答案.
,列出关于α的方程,求解即可得到答案;(Ⅱ)设x1 , x2∈(0,+∞),且x1<x2 , 作差f(x1)﹣f(x2)化简到能直接判断符号为止,利用函数单调性的定义,即可证得答案.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1 , AB,BB1 , B1C1的中点,则异面直线EF与GH所成的角等于 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a为实数,f(x)=(x2﹣4)(x﹣a).
(1)求导数f′(x);
(2)若f′(﹣1)=0,求f(x)在[﹣2,2]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3},N={1,2,3,4},定义函数f:M→N.若点A(1,f(1))、B(2,f(2))、C(3,f(3)),△ABC的外接圆圆心为D,且 ![]() ,则满足条件的函数f(x)有( )
,则满足条件的函数f(x)有( )
A.6个
B.10个
C.12个
D.16个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形ABCD的边AB=m,BC=4,PA⊥平面ABCD,PA=3,现有数据:
① ![]() ;②m=3;③m=4;④
;②m=3;③m=4;④ ![]() .若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )
.若在BC边上存在点Q(Q不在端点B、C处),使PQ⊥QD,则m可以取( )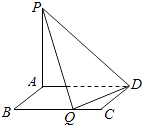
A.①②
B.①②③
C.②④
D.①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com