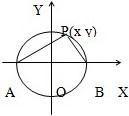
分析:要证PA与PB垂直,即要求出PA的斜率和PB的斜率,把两个斜率相乘得到乘积为-1,所以以AB所在的直线为x轴,圆心为坐标原点建立平面直角坐标系,则得到A、B的坐标,设P(x,y),表示出PA与PB的斜率相乘,把P坐标代入圆的方程化简可得乘积为-1即可得证.
解答:证明:将圆的直径AB所在的直线取为X轴,圆心作为原点,不妨设定圆的半径为1,于是圆的方程是x
2+y
2=1.
A、B的坐标是A(-1,0)、B(1,0).
设P(x,y)是圆上任一点,则有y
2=1-x
2.
∵PA的斜率为
k1=,PB的斜率为
k2=,
∴
k1k2===-1∴PA⊥PB,∠APB为直角.
点评:此题为一道证明题,要求学生掌握两直线垂直的条件为斜率乘积为-1,会利用解析的方法证明数学问题.