
已知一个关于正整数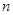 的命题
的命题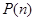 满足“若
满足“若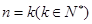 时命题
时命题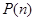 成立,则
成立,则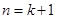 时命题
时命题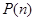 也成立”.有下列判断:
也成立”.有下列判断:
(1)当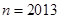 时命题
时命题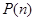 不成立,则
不成立,则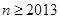 时命题
时命题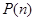 不成立;
不成立;
(2)当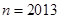 时命题
时命题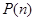 不成立,则
不成立,则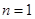 时命题
时命题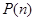 不成立;
不成立;
(3)当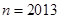 时命题
时命题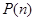 成立,则
成立,则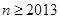 时命题
时命题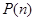 成立;
成立;
(4)当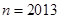 时命题
时命题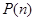 成立,则
成立,则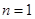 时命题
时命题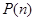 成立.
成立.
其中正确判断的序号是 .(写出所有正确判断的序号)
科目:高中数学 来源: 题型:填空题
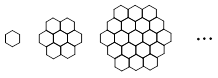
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图. 其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以 表示第
表示第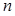 幅图的蜂巢总数.则
幅图的蜂巢总数.则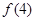 =_____;
=_____; =___________.
=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com