
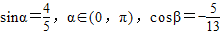 ,β是第三象限角,求cos(α-β)的值.
,β是第三象限角,求cos(α-β)的值.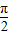 ,π)时,根据sinα=
,π)时,根据sinα= ,求得 cosα 的值.又由cosβ=
,求得 cosα 的值.又由cosβ=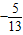 ,β是第三象限角,求得sinβ 的值,由cos(α-β)=cosαcosβ+sinαsinβ求的结果.②当α∈(0,
,β是第三象限角,求得sinβ 的值,由cos(α-β)=cosαcosβ+sinαsinβ求的结果.②当α∈(0, )时,同理求的cos(α-β )的值.
)时,同理求的cos(α-β )的值. ,π)时,且sinα=
,π)时,且sinα= ,得cosα=
,得cosα= ,
, ,β是第三象限角,得sinβ=
,β是第三象限角,得sinβ= =
=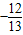 .
. .
. )时,且sinα=
)时,且sinα= ,得cosα=
,得cosα=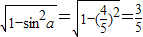 ,
, ,β是第三象限角,得sinβ=
,β是第三象限角,得sinβ=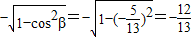 .
. .
.

 53随堂测系列答案
53随堂测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com