
【题目】已知函数f(x)= ![]() sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为
sinx+cosωx(ω>0)的图象与x轴交点的横坐标依次构成一个公差为 ![]() 的等差数列,把函数f(x)的图象沿x轴向左平移
的等差数列,把函数f(x)的图象沿x轴向左平移 ![]() 个单位,得到函数g(x)的图象,则( )
个单位,得到函数g(x)的图象,则( )
A.g(x)是奇函数
B.g(x)关于直线x=﹣ ![]() 对称
对称
C.g(x)在[ ![]() ,
, ![]() ]上是增函数
]上是增函数
D.当x∈[ ![]() ,
, ![]() ]时,g(x)的值域是[2,1]
]时,g(x)的值域是[2,1]
【答案】D
【解析】解:f(x)= ![]() sinx+cosωx(ω>0),
sinx+cosωx(ω>0),
化简得:f(x)=2sin(x+ ![]() ),
),
∵图象与x轴交点的横坐标依次构成一个公差为 ![]() 的等差数列,可知周期为π
的等差数列,可知周期为π
∴T=π= ![]() ,解得ω=2.
,解得ω=2.
那么:f(x)=2sin(2x+ ![]() ),图象沿x轴向左平移
),图象沿x轴向左平移 ![]() 个单位,得:2sin[2(x+
个单位,得:2sin[2(x+ ![]() )+
)+ ![]() ]=2cos2x.
]=2cos2x.
∴g(x)=2cos2x,故g(x)是偶函数,在区间[0, ![]() ]单调减函数.所以A,C不对.
]单调减函数.所以A,C不对.
对称轴方程为x= ![]() (k=Z),检验B不对.
(k=Z),检验B不对.
当x∈[ ![]() ,
, ![]() ]时,那么2x∈[
]时,那么2x∈[ ![]() ,
, ![]() ],g(x)的最大值为1,最小值为﹣2,故值域为[﹣2,1].D正确.
],g(x)的最大值为1,最小值为﹣2,故值域为[﹣2,1].D正确.
故选:D.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2–2x+2.
(1)求函数f(x)的解析式;
(2)当x∈[m,n]时,f(x)的取值范围为[2m,2n],试求实数m,n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市![]() 年
年![]() 月
月![]() 日至
日至![]() 日的空气质量指数趋势图,某人随机选择
日的空气质量指数趋势图,某人随机选择![]() 年
年![]() 月
月![]() 日至
日至![]() 月
月![]() 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留![]() 天.
天.

(1)求此人到达当日空气质量指数大于![]() 的概率;
的概率;
(2)设![]() 是此人停留期间空气质量指数小于
是此人停留期间空气质量指数小于![]() 的天数,求
的天数,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
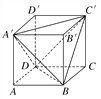
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户,为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元)
(I)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一张坐标纸上已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且直线
两点,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() .
.
(1)求![]() 的值并求函数
的值并求函数![]() 的值域;
的值域;
(2)若关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为
的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张经营某一消费品专卖店,已知该消费品的进价为每件40元,该店每月销售量(百件)与销售单价x(元/件)之间的关系用下图的一折线表示,职工每人每月工资为1000元,该店还应交付的其它费用为每月10000元.

(1)把y表示为x的函数;
(2)当销售价为每件50元时,该店正好收支平衡(即利润为零),求该店的职工人数;
(3)若该店只有20名职工,问销售单价定为多少元时,该专卖店可获得最大月利润?(注:利润=收入-支出)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com