
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
科目:高中数学 来源: 题型:
【题目】某种商品的市场需求量![]() (万件)、市场供应量
(万件)、市场供应量![]() (万件)与市场价格
(万件)与市场价格![]() (元/件)分别近似地满足下列关系:
(元/件)分别近似地满足下列关系: ![]() ,
, ![]() .当
.当![]() 时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.
(1)求平衡价格和平衡需求量;
(2)若该商品的市场销售量![]() (万件)是市场需求量
(万件)是市场需求量![]() 和市场供应量
和市场供应量![]() 两者中的较小者,该商品的市场销售额
两者中的较小者,该商品的市场销售额![]() (万元)等于市场销售量
(万元)等于市场销售量![]() 与市场价格
与市场价格![]() 的乘积.
的乘积.
①当市场价格![]() 取何值时,市场销售额
取何值时,市场销售额![]() 取得最大值;
取得最大值;
②当市场销售额![]() 取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
取得最大值时,为了使得此时的市场价格恰好是新的市场平衡价格,则政府应该对每件商品征税多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3 ![]() ,4),它的渐近线方程为y=±
,4),它的渐近线方程为y=± ![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
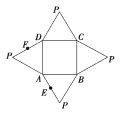
【题目】下图是一几何体的平面展开图,其中四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为全等的等边三角形,
为全等的等边三角形, ![]() 分别为
分别为![]() 的中点.在此几何体中,下列结论中错误的为( )
的中点.在此几何体中,下列结论中错误的为( )
A. 直线![]() 与直线
与直线![]() 共面 B. 直线
共面 B. 直线![]() 与直线
与直线![]() 是异面直线
是异面直线
C. 平面![]() 平面
平面![]() D. 面
D. 面![]() 与面
与面![]() 的交线与
的交线与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆 ![]() 上任取一点
上任取一点 ![]() ,点
,点 ![]() 在
在 ![]() 轴的正射影为点
轴的正射影为点 ![]() ,当点
,当点 ![]() 在圆上运动时,动点
在圆上运动时,动点 ![]() 满足
满足 ![]() ,动点
,动点 ![]() 形成的轨迹为曲线
形成的轨迹为曲线 ![]() .
.
(Ⅰ)求曲线 ![]() 的方程;
的方程;
(Ⅱ)点 ![]() 在曲线
在曲线 ![]() 上,过点
上,过点 ![]() 的直线
的直线 ![]() 交曲线
交曲线 ![]() 于
于 ![]() 两点,设直线
两点,设直线 ![]() 斜率为
斜率为 ![]() ,直线
,直线 ![]() 斜率为
斜率为 ![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家扩大内需的政策,某厂家拟在2016年举行某一产品的促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用t(t≥0)万元满足x=4﹣ ![]() (k为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
(k为常数).如果不搞促销活动,则该产品的年销量只能是1万件.已知2016年生产该产品的固定投入为6万元,每生产1万件该产品需要再投入12万元,厂家将每件产品的销售价格定为每件产品平均生产投入成本的1.5倍(生产投入成本包括生产固定投入和生产再投入两部分).
(1)求常数k,并将该厂家2016年该产品的利润y万元表示为年促销费用t万元的函数;
(2)该厂家2016年的年促销费用投入多少万元时,厂家利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com