
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据系统抽样的定义,可判断①;根据特称命题的否定,可判断②;根据正态分布的对称性,可判断③;根据相关系数的意义,可判断④.
解答 解:对于①,从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是系统抽样,故错误;
对于②,命题p:?x∈R,使得x2+x+1<0.则¬p:?x∈R,均有x2+x+1≥0,故正确;
对于③,设随机变量 X~N(1,σ2),若P(0<X<1)=0.35,则P(1<X<2)=0.35,则P(0<X<2)=0.7,故正确;
对于④,两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1,故错误.
故真命题的个数为2个,
故选:B.
点评 本题以命题的真假判断为载体,考查了抽样方法,命题否定,正态分布,相关系数等知识点,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥8或m≤-2 | B. | m≥8 | C. | m≤-2 | D. | -2≤x≤8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<2 | B. | k≤2 | C. | .0≤k<2 | D. | 0≤k≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
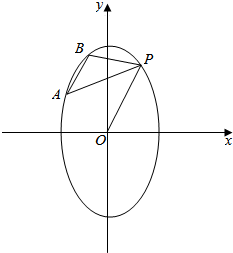 点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.
点P在椭圆3x2+y2=12上,OP倾斜角为60°,AB∥OP,A,B在椭圆上且都在x轴上方,求△ABP面积的最大值及此时直线AB的方程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. | 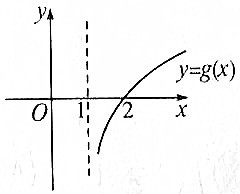 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形.已知AP=PB=AD=2,PD=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com