练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知两曲线f（x）=cosx，g（x）= sinx，x∈（0， ）相交于点A．若两曲线在点A处的切线与x轴分别相交于B，C两点，则线段BC的长为 ．

    【答案】
    【解析】解：由f（x）=g（x），即cosx= sinx，x∈（0， ），可得tanx= ，解得x= ，
    即有A（ ， ），
    由f′（x）=﹣sinx，g′（x）= cosx，
    可得两曲线在点A处的切线斜率分别为﹣ ， ，
    可得切线的方程分别为y﹣ =﹣ （x﹣ ），
    y﹣ = （x﹣ ），
    再令y=0，可得xB= + ，xC= ﹣ ，
    则|BC|=|xB﹣xC|= ．
    故答案为： ．
    由f（x）=g（x），运用同角的商数关系，求得A的坐标，求出f（x），g（x）的导数，可得切线的斜率，由点斜式方程可得切线的方程，令y=0，可得B，C的坐标，由两点的距离公式计算即可得到所求值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}的各项均为不等于1的正数，数列{bn}满足bn＝lgan，b3＝18，b6＝12，则数列{bn}的前n项和的最大值等于(　　)

    A. 126 B. 130 C. 132 D. 134

    【答案】C

    【解析】

    由题意可知，lga3=b3，lga6=b6再由b3，b6，用a1和q表示出a3和b6，进而求得q和a1，根据{an}为正项等比数列推知{bn}为等差数列，进而得出数列bn的通项公式和前n项和，可知Sn的表达式为一元二次函数，根据其单调性进而求得Sn的最大值．

    由题意可知，lga3=b3，lga6=b6．

    又∵b3=18，b6=12，则a1q2=1018，a1q5=1012，

    ∴q3=10﹣6．

    即q=10﹣2，∴a1=1022．

    又∵{an}为正项等比数列，

    ∴{bn}为等差数列，

    且d=﹣2，b1=22．

    故bn=22+（n﹣1）×（﹣2）=﹣2n+24．

    ∴Sn=22n+×（﹣2）

    =﹣n2+23n=，又∵n∈N*，故n=11或12时，（Sn）max=132．

    故答案为：C.

    【点睛】

    这个题目考查的是等比数列的性质和应用；解决等差等比数列的小题时，常见的思路是可以化基本量，解方程；利用等差等比数列的性质解决题目；还有就是如果题目中涉及到的项较多时，可以观察项和项之间的脚码间的关系，也可以通过这个发现规律。

    【题型】单选题
    【结束】
    12

    【题目】已知数列是递增数列，且对，都有，则实数的取值范围是

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着生活水平的提高，越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣，下图为其等高条形图：

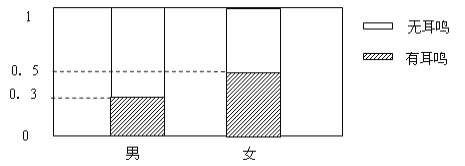
    绘出2×2列联表；

    ②根据列联表的独立性检验，能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系？

    0.025

    0.010

    0.005

    0.001

    5.024

    6.635

    7.879

    10.828

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2﹣ax﹣alnx（a∈R），g（x）=﹣x3+ x2+2x﹣6，g（x）在[1，4]上的最大值为b，当x∈[1，+∞）时，f（x）≥b恒成立，则a的取值范围（ ）
    A.a≤2
    B.a≤1
    C.a≤﹣1
    D.a≤0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（sinx，1）， = ，函数f（x）= 的最大值为6．
    （1）求A；
    （2）将函数f（x）的图象向左平移 个单位，再将所得图象上各点的横坐标缩短为原来的 倍，纵坐标不变，得到函数y=g（x）的图象．求g（x）在[0， ]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的不等式x2﹣4x+t≤0的解集为A，若（﹣∞，t]∩A≠，则实数t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α，β∈（0， ）且sin（α+2β）=
    （1）若α+β= ，求sinβ的值；
    （2）若sinβ= ，求cosα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，a，b，c分别是A，B，C的对边，（2a﹣c）cosB﹣bcosC=0．
    （1）求角B的大小；
    （2）设函数f（x）=2sinxcosxcosB﹣ cos2x，求函数f（x）的最大值及当f（x）取得最大值时x的值．

    查看答案和解析>>

    同步练习册答案