练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】自湖北武汉爆发新型冠状病毒惑染的肺炎疫情以来，武汉医护人员和医疗、生活物资严重缺乏，全国各地纷纷驰援.截至1月30日12时，湖北省累计接收捐赠物资615.43万件，包括医用防护服2.6万套N95口軍47.9万个，医用一次性口罩172.87万个，护目镜3.93万个等.中某运输队接到给武汉运送物资的任务，该运输队有8辆载重为6t的A型卡车，6辆载重为10t的B型卡车，10名驾驶员，要求此运输队每天至少运送720t物资.已知每辆卡车每天往返的次数：A型卡车16次，B型卡车12次；每辆卡车每天往返的成本：A型卡车240元，B型卡车378元.求每天派出A型卡车与B型卡车各多少辆，运输队所花的成本最低？

    【答案】每天派出A型卡车辆，派出B型卡车辆，运输队所花成本最低

    【解析】

    设每天派出A型卡车辆，则派出B型卡车辆，由题意列出约束条件，作出可行域，求出使目标函数取最小值的整数解，即可得解.

    设每天派出A型卡车辆，则派出B型卡车辆，运输队所花成本为元，

    由题意可知，，

    整理得，

    目标函数，

    如图所示，为不等式组表示的可行域，

    由图可知，当直线经过点时，最小，

    解方程组，解得，，

    然而，故点不是最优解.

    因此在可行域的整点中，点使得取最小值，

    即，

    故每天派出A型卡车辆，派出B型卡车辆，运输队所花成本最低.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】生男生女都一样，女儿也是传后人.由于某些地区仍然存在封建传统思想，头胎的男女情况可能会影响生二孩的意愿，现随机抽取某地200户家庭进行调查统计.这200户家庭中，头胎为女孩的频率为0.5，生二孩的频率为0.525，其中头胎生女孩且生二孩的家庭数为60.

    （1）完成下列列联表，并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关；

    生二孩

    不生二孩

    合计

    头胎为女孩

    60

    头胎为男孩

    合计

    200

    （2）在抽取的200户家庭的样本中，按照分层抽样的方法在生二孩的家庭中抽取了7户，进一步了解情况，在抽取的7户中再随机抽取4户，求抽到的头胎是女孩的家庭户数的分布列及数学期望.

    附：

    0.15

    0.05

    0.01

    0.001

    2.072

    3.841

    6.635

    10.828

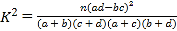    （其中）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，是等边三角形，点是上的一点，平面平面，，，，，.

    （Ⅰ）若点是的中点，求证：平面平面；

    （Ⅱ）若，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图，90后从事互联网行业岗位分布条形图，则下列结论中不正确的是（ ）

    注：90后指1990年及以后出生，80后指1980-1989年之间出生，80前指1979年及以前出生.

    A.互联网行业从业人员中90后占一半以上

    B.互联网行业中从事技术岗位的人数超过总人数的

    C.互联网行业中从事运营岗位的人数90后比80前多

    D.互联网行业中从事技术岗位的人数90后比80后多

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，（其中e为自然对数的底数），若关于x的方程恰有5个相异的实根，则实数a的取值范围为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左焦点坐标为，，分别是椭圆的左，右顶点，是椭圆上异于，的一点，且，所在直线斜率之积为.

    （1）求椭圆的方程；

    （2）过点作两条直线，分别交椭圆于，两点（异于点）.当直线，的斜率之和为定值时，直线是否恒过定点？若是，求出定点坐标；若不是，请说明理.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题：函数在上单调递增；命题：函数在上单调递减.

    （Ⅰ）若是真命题，求实数的取值范围；

    （Ⅱ）若或为真命题，且为假命题，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿，使房价快速走高，为抑制房价过快上涨，政府从2019年2月开始采用实物补偿方式（以房换房），3月份开始房价得到很好的抑制，房价渐渐回落，以下是2019年2月后该区新建住宅销售均价的数据：

    月份

    3

    4

    5

    6

    7

    价格（百元/平方米）

    83

    82

    80

    78

    77

    （1）研究发现，3月至7月的各月均价（百元/平方米）与月份之间具有较强的线性相关关系，求价格（百元/平方米）关于月份的线性回归方程；

    （2）用表示用（1）中所求的线性回归方程得到的与对应的销售均价的估计值，3月份至7月份销售均价估计值与实际相应月份销售均价差的绝对值记为，即，.若，则将销售均价的数据称为一个“好数据”，现从5个销售均价数据中任取2个，求抽取的2个数据均是“好数据”的概率.

    参考公式：回归方程系数公式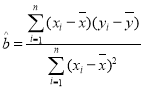，；参考数据：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，四边形为正方形，点为线段上的点，过三点的平面与交于点.将①，②，③中的两个补充到已知条件中，解答下列问题：

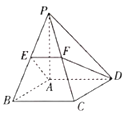
    （1）求平面将四棱锥分成两部分的体积比；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    同步练习册答案