练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，是⊙0直径，是圆周上不同于的任意一点，平面，则四面体的四个面中，直角三角形的个数有（    ）

     

     

    A、个       B、个       C、个        D、个

     

    【答案】

    A

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

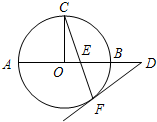    精英家教网A（选修4-1：几何证明选讲）
    如图，AB是⊙O的直径，C，F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．
    求证：DE2=DB•DA．
    B（选修4-2：矩阵与变换）
    求矩阵
    21
    12
    的特征值及对应的特征向量．
    C（选修4-4：坐标系与参数方程）
    已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是
    x=-
    3
    5
    t+2
    y=
    4
    5
    t
    （t为参数）．
    （Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
    （Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
    D（选修4-5：不等式选讲）
    已知m＞0，a，b∈R，求证：(
    a+mb
    1+m
    )2≤
    a2+mb2
    1+m
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

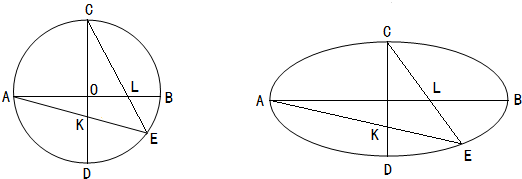    （1）如图，设圆O：x2+y2=a2的两条互相垂直的直径为AB、CD，E在弧BD上，AE交CD于K，CE交AB于L，求证：(
    EK
    AK
    )2+(
    EL
    CL
    )2    为定值
    （2）将椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）与x2+y2=a2相类比，请写出与（1）类似的命题，并证明你的结论．
    （3）如图，若AB、CD是过椭圆
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）中心的两条直线，且直线AB、CD的斜率积kAB•kCD=-
    b2
    a2
    ，点E是椭圆上异于A、C的任意一点，AE交直线CD于K，CE交直线AB于L，求证：(
    EK
    AK
    )2+(
    EL
    CL
    )2    为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

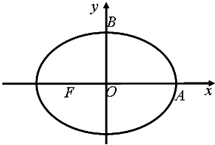    精英家教网如图，点F是椭圆W：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的左焦点，A、B分别是椭圆的右顶点与上顶点，椭圆的离心率为
    1
    2
    ，三角形ABF的面积为
    3
    		3
    2
    ，
    （Ⅰ）求椭圆W的方程；
    （Ⅱ）对于x轴上的点P（t，0），椭圆W上存在点Q，使得PQ⊥AQ，求实数t的取值范围；
    （Ⅲ）直线l：y=kx+m（k≠0）与椭圆W交于不同的两点M、N （M、N异于椭圆的左右顶点），若以MN为直径的圆过椭圆W的右顶点A，求证：直线l过定点，并求出该定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：2010年普通高等学校招生全国统一考试、理科数学(湖北卷) 题型：022

    设a＞0，b＞0，称为a，b的调和平均数．如图，C为线殴AB上的点，且AC＝a，CB＝b，O为AB中点，以AB为直径作半圆．过点C作OD的垂线，垂足为E．连结OD，AD，BD．过点C作OD的垂线，垂足为E．则图中线段OD的长度是a，b的算术平均数，线段________的长度是a，b的几何平均数，线段________的长度是a，b的调和平均数．

    查看答案和解析>>

    同步练习册答案