
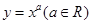 图像经过不等式组
图像经过不等式组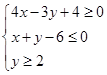 表示的区域,则a的取值范围是
表示的区域,则a的取值范围是A.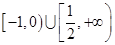 | B. |
C. | D.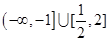 |
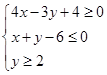 表示的区域,
表示的区域,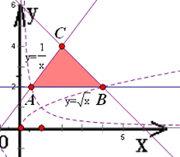
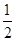 ,2),B(4,2),C(2,4)作出函数函数y=xa的图象,当a>0时,函数图象经过点B(4,2)时,表达式为y=x
,2),B(4,2),C(2,4)作出函数函数y=xa的图象,当a>0时,函数图象经过点B(4,2)时,表达式为y=x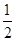 ,在此基础上让a值变大时,图象在第一象限的图象变得陡峭,因为图象总是经过点(1,1),所以曲线y=xa必经过点(1,1)上方,位于△ABC内部的区域,故曲线
,在此基础上让a值变大时,图象在第一象限的图象变得陡峭,因为图象总是经过点(1,1),所以曲线y=xa必经过点(1,1)上方,位于△ABC内部的区域,故曲线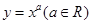 始终经过△ABC及其内部;当a<0时,函数图象经过点A(
始终经过△ABC及其内部;当a<0时,函数图象经过点A(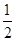 ,2)时,表达式为y=x-1,在此基础上让a值变小时,图象在第一象限的图象也变陡峭,由函数y=xa为减函数,可得始终经过△ABC及其内部.由以上的讨论,可得a≥
,2)时,表达式为y=x-1,在此基础上让a值变小时,图象在第一象限的图象也变陡峭,由函数y=xa为减函数,可得始终经过△ABC及其内部.由以上的讨论,可得a≥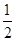 或a≤-1故选B
或a≤-1故选B

科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
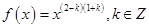 ,且
,且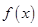 在
在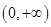 上单调递增.
上单调递增.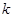 的值,并写出相应的函数
的值,并写出相应的函数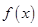 的解析式;
的解析式;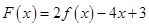 在区间
在区间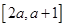 上不单调,求实数
上不单调,求实数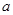 的取值范围;
的取值范围;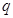 ,使函数
,使函数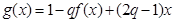 在区间
在区间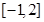 上的值域为
上的值域为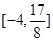 若存在,求出
若存在,求出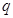 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.8x-y-30=0 | B.x-4y+4=0 |
| C.8x+y-30=0 | D.x+4y+4=0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
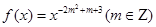 为偶函数,且在
为偶函数,且在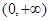 上为增函数.
上为增函数.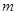 的值,并确定
的值,并确定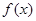 的解析式;
的解析式;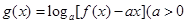 且
且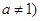 ,是否存在实数
,是否存在实数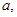 使
使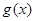 在区间
在区间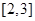 上的最大值为2,若存在,求出
上的最大值为2,若存在,求出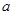 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com