
【题目】在![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,如图1.以
,如图1.以![]() 为折痕将
为折痕将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
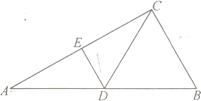
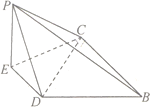
如图1 如图2
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)见解析;(2)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】
(1)在题图1中,可证![]() ,在题图2中,
,在题图2中,![]() 平面
平面![]() .进而得到
.进而得到![]() 平面
平面![]() .从而证得平面
.从而证得平面![]() 平面
平面![]() ;
;
(2)可证得![]() 平面
平面![]() .
. ![]() .则以
.则以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线
轴的正方向建立如图所示的空间直角坐标系,利用空间向量可求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)证明:在题图1中,因为![]() ,且
,且![]() 为
为![]() 的中点.由平面几何知识,得
的中点.由平面几何知识,得![]() .
.
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]()
在题图2中,![]() ,
,![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)解:因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() .
.
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
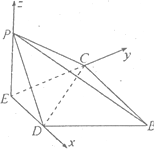
轴、![]() 轴的正方向建立如图所示的空间直角坐标系
轴的正方向建立如图所示的空间直角坐标系
在题图1中,设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则 ,即
,即![]()
令![]() ,则
,则![]() .所以
.所以![]() .
.
设![]() 与
与![]() 平面所成的角为
平面所成的角为![]() ,
,
则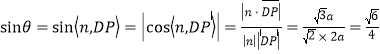 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,边a、b、c分别是角A、B、C的对边,且满足bcosC=(3a-c)cosB
(1)求cosB
(2)若△ABC的面积为4![]() ,b=4
,b=4![]() ,求△ABC的周长
,求△ABC的周长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点.求证:

(1)DE=DA;
(2)平面BDM⊥平面ECA;
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是首项
是首项![]() 的等差数列,设
的等差数列,设![]() .
.
(1)求证:![]() 是等比数列;
是等比数列;
(2)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)在(2)的条件下,记![]() ,若对任意正整数
,若对任意正整数![]() ,不等式
,不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影为点
上的正投影为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
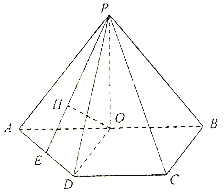
(1)求证:![]() 为
为![]() 中点;
中点;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com