
【题目】下面几种推理过程是演绎推理的是 ( ).
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列{an}中,a1=1,![]() ,
,![]() ,
,![]() ,由此归纳出{an}的通项公式
,由此归纳出{an}的通项公式
科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.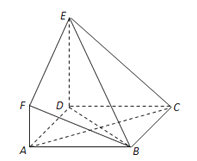
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )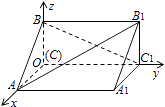
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有2只红球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同.
(Ⅰ)若抽取后又放回,抽3次.
(ⅰ)分别求恰2次为红球的概率及抽全三种颜色球的概率;
(ⅱ)求抽到红球次数![]() 的数学期望及方差.
的数学期望及方差.
(Ⅱ)若抽取后不放回,写出抽完红球所需次数![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E= ![]() .
.
(Ⅰ)证明:A1D⊥平面A1BC;
(Ⅱ)求二面角A﹣BD﹣B1的平面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com