
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
【答案】
(1)解:行车所用时间为 ![]() ,
,
根据汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元,可得行车总费用:
)升,司机的工资是每小时14元,可得行车总费用:
y= ![]() =
= ![]() (50≤x≤100)
(50≤x≤100)
(2)解:y= ![]() ≥26
≥26 ![]() ,当且仅当
,当且仅当 ![]() ,即
,即 ![]() 时,等号成立
时,等号成立
∴当 ![]() 时,这次行车的总费用最低,最低费用为26
时,这次行车的总费用最低,最低费用为26 ![]() 元
元
【解析】(1)求出车所用时间,根据汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元,可得行车总费用;(2)利用基本不等式,即可求得这次行车的总费用最低.
)升,司机的工资是每小时14元,可得行车总费用;(2)利用基本不等式,即可求得这次行车的总费用最低.
【考点精析】解答此题的关键在于理解基本不等式在最值问题中的应用的相关知识,掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.


科目:高中数学 来源: 题型:
【题目】某市有![]() 三所高校,其学生会学习部有“干事”人数分别为
三所高校,其学生会学习部有“干事”人数分别为![]() ,现采用分层抽样的方法从这些“干事”中抽取
,现采用分层抽样的方法从这些“干事”中抽取![]() 名进行“大学生学习部活动现状”调查.
名进行“大学生学习部活动现状”调查.
(1)求应从![]() 这三所高校中分别抽取的“干事”人数;
这三所高校中分别抽取的“干事”人数;
(2)若从抽取的![]() 名干事中随机选两名干事,求选出的
名干事中随机选两名干事,求选出的![]() 名干事来自同一所高校的概率.
名干事来自同一所高校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F为棱AD、AB的中点. 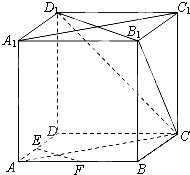
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=![]() ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考浙江理数】如图,设椭圆![]() (a>1).
(a>1).
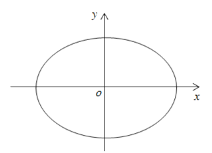
(I)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值
范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),则下面结论错误的是( )
)(x∈R),则下面结论错误的是( )
A.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
C.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
D.函数f(x)的图象是由函数y= ![]() sin2x的图象向右平移
sin2x的图象向右平移 ![]() 个单位而得到
个单位而得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com