
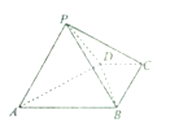
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,PA=PD=CD=BC=1.
,PA=PD=CD=BC=1.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)推导出AD⊥BD,PA⊥BD,从而BD⊥平面PAD,由此能证明平面PAD⊥平面ABCD.
(2)取AD中点O,连结PO,则PO⊥AD,以O为坐标原点,以过点O且平行于BC的直线为x轴,过点O且平行于AB的直线为y轴,直线PO为z轴,建立空间直角坐标系,利用空间向量法能求出直线PA与平面PBC所成角的正弦值.
(1)∵AB∥CD,∠BCD![]() ,PA=PD=CD=BC=1,
,PA=PD=CD=BC=1,
∴BD![]() ,∠ABC
,∠ABC![]() ,
,![]() ,∴
,∴![]() ,
,
∵AB=2,∴AD![]() ,∴AB2=AD2+BD2,∴AD⊥BD,
,∴AB2=AD2+BD2,∴AD⊥BD,
∵PA⊥BD,PA∩AD=A,∴BD⊥平面PAD,
∵BD平面ABCD,∴平面PAD⊥平面ABCD.
(2)取AD中点O,连结PO,则PO⊥AD,且PO![]() ,
,
由平面PAD⊥平面ABCD,知PO⊥平面ABCD,
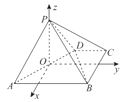
以O为坐标原点,以过点O且平行于BC的直线为x轴,过点O且平行于AB的直线为y轴,
直线PO为z轴,建立如图所示的空间直角坐标系,
则A(![]() ,0),B(
,0),B(![]() ,0),C(
,0),C(![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
![]() (﹣1,0,0),
(﹣1,0,0),![]() (
(![]() ,
,![]() ),
),
设平面PBC的法向量![]() (x,y,z),
(x,y,z),
则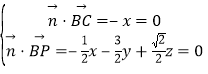 ,取z
,取z![]() ,得
,得![]() (0,
(0,![]() ,
,![]() ),
),
∵![]() (
(![]() ,
,![]() ),
),
∴cos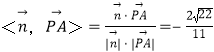 ,
,
∴直线PA与平面PBC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2012年“双节”期间,高速公路车辆较多![]() 某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
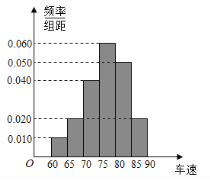
,![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
![]() 某调查公司在采样中,用到的是什么抽样方法?
某调查公司在采样中,用到的是什么抽样方法?
![]() 求这40辆小型车辆车速的众数和中位数的估计值.
求这40辆小型车辆车速的众数和中位数的估计值.
![]() 若从车速在
若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(1)求出表中x,y的值;
(2)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
附:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,过点
,过点![]() 向圆
向圆![]() 引两条切线
引两条切线![]() ,
,![]() ,切点为
,切点为![]() ,
,![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,则直线
,则直线![]() 的方程为____________;若
的方程为____________;若![]() 为直线
为直线![]() 上一动点,则直线
上一动点,则直线![]() 经过定点__________.
经过定点__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆的标准方程:
(1)焦点在y轴上,焦距是4,且经过点M(3,2);
(2)c∶a=5∶13,且椭圆上一点到两焦点的距离的和为26.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子阅读的普及,传统纸质媒体遭受到了强烈的冲击.某杂志社近9年来的纸质广告收入如下表所示:

根据这9年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.243;
作线性相关性检验,求得样本相关系数的绝对值为0.243;
根据后5年的数据,对![]() 和
和![]() 作线性相关性检验,求得样本相关系数的绝对值为0.984.
作线性相关性检验,求得样本相关系数的绝对值为0.984.
(1)如果要用线性回归方程预测该杂志社2019年的纸质广告收入,现在有两个方案,
方案一:选取这9年数据进行预测,方案二:选取后5年数据进行预测.
从实际生活背景以及线性相关性检验的角度分析,你觉得哪个方案更合适?
附:相关性检验的临界值表:
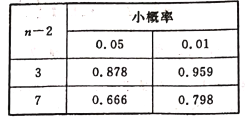
(2)某购物网站同时销售某本畅销书籍的纸质版本和电子书,据统计,在该网站购买该书籍的大量读者中,只购买电子书的读者比例为![]() ,纸质版本和电子书同时购买的读者比例为
,纸质版本和电子书同时购买的读者比例为![]() ,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
,现用此统计结果作为概率,若从上述读者中随机调查了3位,求购买电子书人数多于只购买纸质版本人数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面命题正确的是( )
A.“![]() ”是“
”是“![]() ”的 充 分不 必 要条件
”的 充 分不 必 要条件
B.命题“若![]() ,则
,则![]() ”的 否 定 是“ 存 在
”的 否 定 是“ 存 在![]() ,则
,则![]() ”.
”.
C.设![]() ,则“
,则“![]() 且
且![]() ”是“
”是“![]() ”的必要而不充分条件
”的必要而不充分条件
D.设![]() ,则“
,则“![]() ”是“
”是“![]() ”的必要 不 充 分 条件
”的必要 不 充 分 条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义域R上的奇函数,且在R上是单调递增函数,函数
为定义域R上的奇函数,且在R上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com