
分析 根据指数函数的图象和性质,可判断①;根据抽象函数的定义域,可判断②;根据函数的奇偶性,可判断③;根据对数的运算性质,可判断④.
解答 解:当x=1时,ax-1+3=4恒成立,故函数f(x)=ax-1+3(a>0且a≠1)的图象一定过点P(1,4),故①正确;
函数f(x-1)的定义域是(1,3),则x-1∈(0,2),即函数f(x)的定义域为(0,2),故②错误;
令g(x)=x5+ax3-bx,则函数为奇函数,由f(2)=-8,得g(2)=0,故g(-2)=0,故f(2)=-8,故③正确;
若2a=3b=k,则a=log2k,b=log3k,则$\frac{1}{a}$=logk2,$\frac{2}{b}$=2logk3,则$\frac{1}{a}$+$\frac{2}{b}$=logk18=-1,则k=-$\frac{1}{18}$,故④错误;
故正确的命题有:①③,
故答案为:①③
点评 本题以命题的真假判断为载体,考查了指数函数的图象和性质,抽象函数的定义域,函数的奇偶性,对数的运算性质,难度中档.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
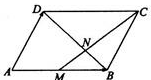 已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,M为AB中点,N为BD靠近B的三等分点.
已知平行四边形ABCD中,$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{AB}$=$\overrightarrow{b}$,M为AB中点,N为BD靠近B的三等分点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com