
【题目】对绵阳南山实验学校的500名教师的年龄进行统计分析,年龄的频率分布直方图如图所示,规定年龄在![]() 内的为青年教师,
内的为青年教师,![]() 内的为中年教师,
内的为中年教师,![]() 内的为老年教师.
内的为老年教师.
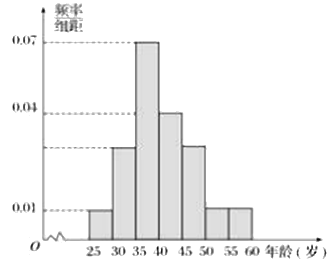
(1)求年龄![]() ,
,![]() 内的教师人数;
内的教师人数;
(2)现用分层抽样的方法从中、青年中抽取18人进行同课异构课堂展示,求抽到年龄在![]() 内的人数.
内的人数.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某工厂2万元设计了某款式的服装,根据经验,每生产1百套该款式服装的成本为1万元,每生产![]() (百套)的销售额(单位:万元)
(百套)的销售额(单位:万元)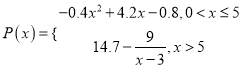 .
.
(1)若生产6百套此款服装,求该厂获得的利润;
(2)该厂至少生产多少套此款式服装才可以不亏本?
(3)试确定该厂生产多少套此款式服装可使利润最大,并求最大利润.(注:利润=销售额-成本,其中成本=设计费+生产成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]()
![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为正三角形,
为正三角形,![]() 是棱
是棱![]() 上的一点(异于端点).
上的一点(异于端点).
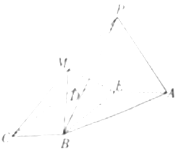
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)是否存在点![]() ,使二面角
,使二面角![]() 的大小为30°.若存在,求出点
的大小为30°.若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数![]() 中定义一种新运算:
中定义一种新运算: ![]() ,对实数
,对实数![]() 经过运算
经过运算![]() 后是一个确定的唯一的实数。
后是一个确定的唯一的实数。![]() 运算有如下性质:(1)对任意实数
运算有如下性质:(1)对任意实数![]() ,
, ![]() ;(2)对任意实数
;(2)对任意实数![]() ,
, ![]() 那么:关于函数
那么:关于函数![]() 的性质下列说法正确的是:①函数
的性质下列说法正确的是:①函数![]() 的最小值为3;②函数
的最小值为3;②函数![]() 是偶函数;③函数
是偶函数;③函数![]() 在
在![]() 上为减函数,这三种说法正确的有__________.
上为减函数,这三种说法正确的有__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔参加“全市高中数学竞赛”的选手,某中学举行了一次“数学竞赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() 分)作为样本(样本容量为
分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() 的数据).
的数据).
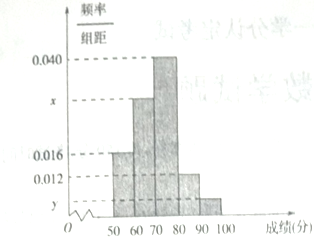
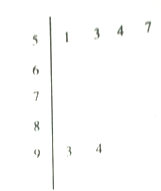
(1)求样本容![]() 和频率分布直方图中
和频率分布直方图中![]() 的值并求出抽取学生的平均分;
的值并求出抽取学生的平均分;
(2)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生参加“全市中数学竞赛”求所抽取的
名学生参加“全市中数学竞赛”求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com