练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

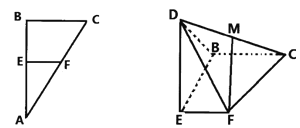
    【题目】如图在直角中，为直角，，，分别为，的中点，将沿折起，使点到达点的位置，连接，，为的中点．

    （Ⅰ）证明：面；

    （Ⅱ）若，求二面角的余弦值．

    【答案】（Ⅰ）详见解析；（Ⅱ）.

    【解析】

    （Ⅰ）取中点，连结、，四边形是平行四边形，由，，得，从而，，求出，由此能证明．

    （Ⅱ）以为原点，、、所在直线分别为，，轴，建立空间直角坐标系，利用向量法能求出二面角的余弦值．

    证明：（Ⅰ ）取中点，连结、，

    ∵ ，，

    ∴ 四边形是平行四边形，

    ∵ ，，，

    ∴ ，

    ∴ ，∴，

    在中，，

    又∵ 为的中点，∴，

    又∵ ，∴．

    解：（Ⅱ）∵，，，

    ∴ ，

    以为原点，、、所在直线分别为，，轴，建立空间直角坐标系，

    设，则，，，，

    ∴ ，，，

    设面的法向量，

    则，取，得，

    同理，得平面的法向量，

    设二面角的平面角为，

    则，

    ∴ 二面角的余弦值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】莆田市是福建省“历史文化名城”之一，也是旅游资源丰富的城市.“九头十八巷”、“二十四景”美如画.某文化传媒公司为了解莆田民众对当地风景民俗知识的了解情况，在全市进行网上问卷（满分100分）调查，民众参与度极高.该公司对得分数据进行统计拟合，认为服从正态分布.

    （1）从参与调查的民众中随机抽取200名作为幸运者，试估算其中得分在75分以上（含75分）的人数（四舍五入精确到1人）；

    （2）在（1）的条件下，为感谢参与民众，该公司组织两种活动，得分在75分以上（含75分）的幸运者选择其中一种活动参与.活动如下：

    活动一 参与一次抽奖.已知抽中价值200元的礼品的概率为，抽中价值420元的礼品的概率为；

    活动二 挑战一次闯关游戏.规则如下：游戏共有三关，闯关成功与否相互独立，挑战者依次闯关，第一关闯关失败者没有获得礼品，第二关起闯关失败者只能获得上一关的礼品，获得的礼品不累计，闯关结束.已知第一关通过的概率为，可获得价值300元的礼品；第二关通过的概率为，可获得价值800元的礼品；第三关通过的概率为，可获得价值1800元的礼品.

    若参与活动的幸运者均选择礼品价值期望值较高的活动，该公司以该期望值为依据，需准备多少元的礼品？

    附：若，则，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知边长为2的正三角形ABE所在的平面与菱形ABCD所在的平面垂直，且，点F是BC上一点，且．

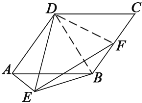
    （1）当时，证明：；

    （2）是否存在一个常数k，使得三棱锥的体积等于四棱锥的体积的，若存在，求出k的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”已成为当下热门的健身方式，小明的微信朋友圈内也有大量好友参与了“微信运动”，他随机选取了其中的40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下：

    0～2000

    2001～5000

    5001～8000

    8001～10000

    男

    1

    2

    3

    6

    8

    女

    0

    2

    10

    6

    2

    （1）若采用样本估计总体的方式，试估计小明的所有微信好友中每日走路步数超过5000步的概率；

    （2）已知某人一天的走路步数超过8000步时被系统评定为“积极型”，否则为“懈怠型”.根据小明的统计完成下面的列联表，并据此判断是否有以上的把握认为“评定类型”与“性别”有关？

    积极型

    懈怠型

    总计

    男

    女

    总计

    附：

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，又在直角坐标系中，曲线的参数方程为（t为参数）.

    （1）求曲线的直角坐标方程和曲线的普通方程；

    （2）已知点在曲线上，点Q在曲线上，若的最小值为，求此时点的直角坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数\.

    （1）若且在处的切线垂直于y轴，求a的值；

    （2）若对于任意，都有恒成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为等差数列的前项和，且，．

    （1）求数列的通项公式；

    （2）若满足不等式的正整数恰有个，求正实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究一种昆虫的产卵数和温度是否有关，现收集了7组观测数据列于下表中，并作出了如图的散点图．

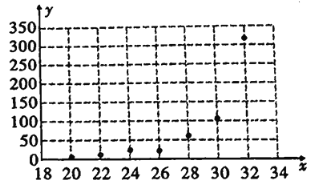
    温度/℃

    20

    22

    24

    26

    28

    30

    32

    产卵数/个

    6

    10

    22

    26

    64

    118

    310

    26

    79．4

    3．58

    112

    11．6

    2340

    35．72

    其中．

    （1）根据散点图判断，与哪一个更适宜作为该昆虫的产卵数与温度的回归方程类型？（给出判断即可，不必说明理由）．

    （2）根据表中数据，建立关于的回归方程；（保留两位有效数字）

    （3）根据关于的回归方程，估计温度为33℃时的产卵数．

    （参考数据：）

    附：对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为．

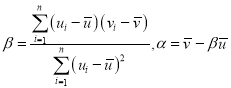    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱中，，，是的中点.

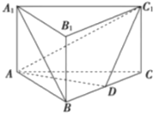
    （1）求证：平面；

    （2）求二面角的余弦值；

    （3）试问线段上是否存在点，使与面所成角的正弦值为？若存在，求出此时的长，若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案