
(本小题满分12分)已知函数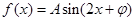
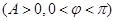 ,当
,当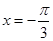 时取得最小值-4.
时取得最小值-4.
(1)求函数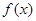 的解析式;
的解析式;
(2)若等差数列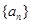 前n项和为
前n项和为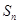 ,且
,且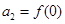 ,
, ,求数列
,求数列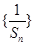 的前n项和
的前n项和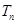 .
.
(1) ;(2)
;(2) .
.
解析试题分析: 本题是三角函数与数列的综合题目,考查三角函数的最值、解析式,数列的通项公式、求和公式等基础知识,考查数形结合思想、转化思想和计算能力.第一问,根据已知条件,当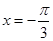 时取得最小值-4,所以数形结合将坐标代入解出
时取得最小值-4,所以数形结合将坐标代入解出 的值,得到函数解析式;第二问,根据第一问的解析式,先求出
的值,得到函数解析式;第二问,根据第一问的解析式,先求出 和
和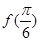 即
即 和
和 的值,利用等差数列的通项公式求出数列
的值,利用等差数列的通项公式求出数列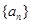 的首项和公差,并求出数列的前n项和
的首项和公差,并求出数列的前n项和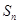 ,用裂项相消法求数列
,用裂项相消法求数列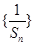 的前n项和.
的前n项和.
试题解析:(1)由题意 时取得最小值-4,
时取得最小值-4, ,
,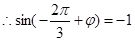 ,
,
又因为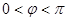 ,
,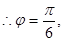 所以
所以 4分
4分
(2)因为 ,
, ,所以
,所以 ,
,
设等差数列公差为 ,则
,则 ,
, 8分
8分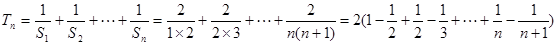
 12分
12分
考点:1.三角函数的最值;2.等差数列的通项公式;3.等差数列的前n项和公式;4.裂项相消法求和.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题.若某地区2012年人口总数为45万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2013年开始到2022年每年人口比上年增加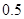 万人,从2023年开始到2032年每年人口为上一年的99%.
万人,从2023年开始到2032年每年人口为上一年的99%.
(1)求实施新政策后第 年的人口总数
年的人口总数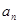 的表达式(注:2013年为第一年);
的表达式(注:2013年为第一年);
(2)若新政策实施后的2013年到2032年人口平均值超过49万,则需调整政策,否则继续实施.问到2032年后是否需要调整政策?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设等差数列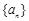 的前
的前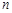 项和为
项和为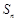 ,已知
,已知 ,
,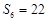 .
.
(1)求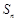 ;
;
(2)若从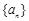 中抽取一个公比为
中抽取一个公比为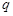 的等比数列
的等比数列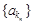 ,其中
,其中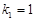 ,且
,且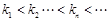 ,
,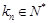 .
.
①当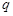 取最小值时,求
取最小值时,求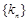 的通项公式;
的通项公式;
②若关于 的不等式
的不等式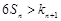 有解,试求
有解,试求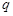 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列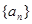 满足
满足 (
( ).
).
(1)若数列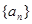 是等差数列,求它的首项和公差;
是等差数列,求它的首项和公差;
(2)证明:数列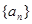 不可能是等比数列;
不可能是等比数列;
(3)若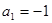 ,
, (
( ),试求实数
),试求实数 和
和 的值,使得数列
的值,使得数列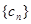 为等比数列;并求此时数列
为等比数列;并求此时数列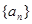 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com