
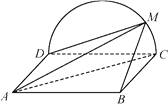
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,
的中点,![]() 与
与![]() 所成角的大小为90°,且
所成角的大小为90°,且![]() .
.
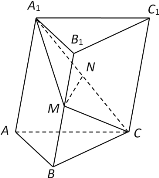
求证:(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,推导出四边形
,推导出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
证明:(1)因为![]() 与
与![]() 所成角的大小为90°,所以
所成角的大小为90°,所以![]() ⊥
⊥![]() ,
,
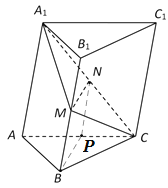
因为![]() ,且N是A1C的中点,所以
,且N是A1C的中点,所以![]() ⊥
⊥![]() .
.
又![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,
故![]() ⊥平面
⊥平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() ⊥平面
⊥平面![]() .
.
(2)取AC中点P,连结NP,BP.
因为N为A1C中点,P为AC中点,所以PN//AA1,且PN![]() AA1.
AA1.
在三棱柱![]() 中,BB1 // AA1,且BB1
中,BB1 // AA1,且BB1![]() AA1.
AA1.
又M为BB1中点,故BM // AA1,且BM![]() AA1.
AA1.
所以PN // BM,且PN![]() BM,于是四边形PNMB是平行四边形,
BM,于是四边形PNMB是平行四边形,
从而MN // BP.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
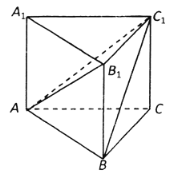
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代科学家祖冲之儿子祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与如图所示的三视图所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
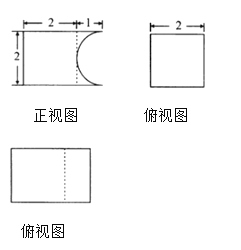
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)当a=![]() 1时,求函数y=f(x)的单调区间;
1时,求函数y=f(x)的单调区间;
(2)求函数y=f(x)的极值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com