
 ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2. [﹣(2x1+2)+(2x2+2)]≥
[﹣(2x1+2)+(2x2+2)]≥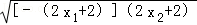 =1,
=1,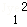 +2x1+a)=(2x1+2)(x﹣x1);
+2x1+a)=(2x1+2)(x﹣x1);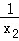 (x﹣x2);
(x﹣x2);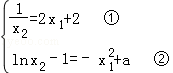 ,
,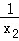 <2,由①②得a=lnx2+(
<2,由①②得a=lnx2+(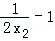 )2﹣1=﹣ln
)2﹣1=﹣ln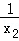 +
+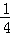 (
(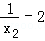 )2﹣1,
)2﹣1,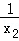 ,则0<t<2,且a=
,则0<t<2,且a=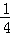 t2﹣t﹣lnt,设h(t)=
t2﹣t﹣lnt,设h(t)=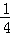 t2﹣t﹣lnt,(0<t<2)
t2﹣t﹣lnt,(0<t<2)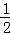 t﹣1﹣
t﹣1﹣ =
=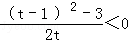 ,∴h(t)在(0,2)为减函数,
,∴h(t)在(0,2)为减函数,

科目:高中数学 来源:不详 题型:解答题
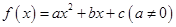 ,且不等式
,且不等式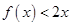 的解集为
的解集为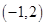 .
.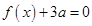 有两个相等的实根,求
有两个相等的实根,求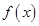 的解析式;
的解析式;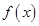 的最小值不大于
的最小值不大于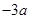 ,求实数
,求实数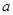 的取值范围;
的取值范围;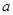 如何取值时,函数
如何取值时,函数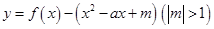 存在零点,并求出零点.
存在零点,并求出零点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,若存在
,若存在 ,使得
,使得 ,则称
,则称 是函数
是函数 的一个不动点,设二次函数
的一个不动点,设二次函数 .
.  时,求函数
时,求函数 的不动点;
的不动点; ,函数
,函数 恒有两个不同的不动点,求实数
恒有两个不同的不动点,求实数 的取值范围;
的取值范围; 的图象上
的图象上 两点的横坐标是函数
两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段
是线段 的垂直平分线,求实数
的垂直平分线,求实数 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com