
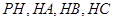 构成,其底端三点
构成,其底端三点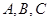 均匀地固定在半径为
均匀地固定在半径为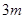 的圆
的圆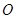 上(圆
上(圆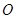 在地面上),
在地面上),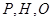 三点相异且共线,
三点相异且共线,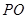 与地面垂直. 现要求点
与地面垂直. 现要求点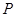 到地面的距离恰为
到地面的距离恰为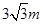 ,记用料总长为
,记用料总长为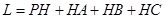 ,设
,设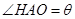 .
.
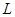 表示为
表示为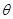 的函数,并注明定义域;
的函数,并注明定义域;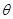 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省? ,
, ;(2)
;(2) .
.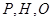 三点相异且共线,
三点相异且共线,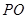 与地面垂直,且三点
与地面垂直,且三点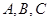 均匀地固定在半径为
均匀地固定在半径为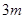 的圆
的圆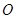 上,所以
上,所以 是全等的直角三角形,从而有
是全等的直角三角形,从而有 ,进而可得
,进而可得 ,再由点
,再由点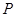 到地面的距离恰为
到地面的距离恰为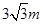 得
得 ;从而由
;从而由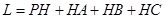 可将L表示为
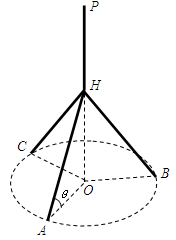
可将L表示为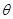 的函数;其定义域由图形可知:
的函数;其定义域由图形可知: ,而当PH最短时角
,而当PH最短时角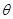 为最大,但由于
为最大,但由于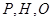 三点相异,所以
三点相异,所以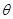 小于该最大值,从而求得其定义域;(2)用料最省,即L取得最小值;由(1)的函数利用导数方法来求使其取得最小值的
小于该最大值,从而求得其定义域;(2)用料最省,即L取得最小值;由(1)的函数利用导数方法来求使其取得最小值的 的值:先求出L的导函数,再令其等于零求出对应的
的值:先求出L的导函数,再令其等于零求出对应的 的值,再讨论函数的单调性就可确定
的值,再讨论函数的单调性就可确定 的值.
的值.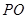 与地面垂直,且
与地面垂直,且 ,则
,则 是全等的直角三角形,又圆
是全等的直角三角形,又圆 的半径为3,
的半径为3, ,
, , 3分
, 3分 ,所以
,所以 , 6分
, 6分 重合,则
重合,则 ,即
,即 ,所以
,所以 ,
, ,
, . 7分
. 7分 ,
, ,当
,当 时,
时, , 11分
, 11分 ,
, ,当
,当 时,
时, ;当
;当 时,
时, ;
; 上单调递减,在
上单调递减,在 上单调递增, 15分
上单调递增, 15分 ,即
,即 时,L有最小值,此时用料最省. 16分
时,L有最小值,此时用料最省. 16分

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:解答题
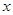 元,则本年度新增用电量
元,则本年度新增用电量 (亿千瓦时)与
(亿千瓦时)与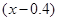 元成反比例.又当
元成反比例.又当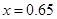 时,
时,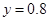 .
. 与
与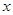 之间的函数关系式;
之间的函数关系式;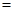 用电量
用电量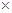 (实际电价-成本价)]
(实际电价-成本价)]查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
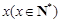 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为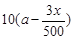 万元
万元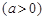 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高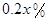 .
.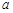 的取值范围是多少?
的取值范围是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式 ,
, 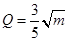 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资 (单位:万元)
(单位:万元) (单位:万元)关于
(单位:万元)关于 的函数关系式,并指明函数定义域;
的函数关系式,并指明函数定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.?x∈R,x2+x+1<0 | B.?x∉R,x2+x+1<0 |
| C.?x∉R,x2+x+1<0 | D.?x∈R,x2+x+1<0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.?x∈R,x3+3x≥0 | B.?x∈R,x3+3x≤0 |
| C.?x∈R,x3+3x≥0 | D.?x∈R,x3+3x≤0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
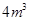 ,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是( )
,高为1m的无盖长方体容器,已知该溶器的底面造价是每平方米20元,侧面造价是是每平方米10元,则该容器的最低总造价是( )| A.80元 | B.120元 | C.160元 | D.240元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com