
(本题12分)已知椭圆 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线 上,求直线AC的方程。
上,求直线AC的方程。
(I)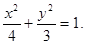 (II)直线AC的方程为
(II)直线AC的方程为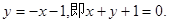
【解析】
试题分析:(I)设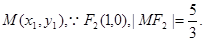 由抛物线定义,
由抛物线定义,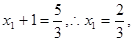
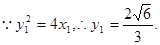 ,
, 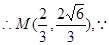 M点C1上,
M点C1上,

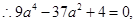
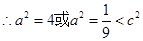 舍去.
舍去.
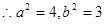
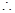 椭圆C1的方程为
椭圆C1的方程为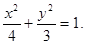
(II)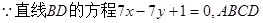 为菱形,
为菱形, ,设直线AC的方程为
,设直线AC的方程为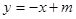

 在椭圆C1上,
在椭圆C1上,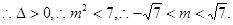 设
设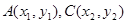 ,则
,则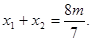
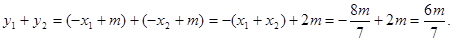
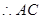 的中点坐标为
的中点坐标为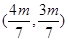 ,由ABCD为菱形可知,点
,由ABCD为菱形可知,点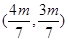 在直线BD:
在直线BD: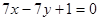 上,
上,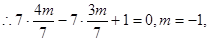
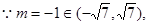 ∴直线AC的方程为
∴直线AC的方程为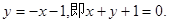
考点:本题主要考查抛物线的定义,椭圆标准方程及几何性质,直线与椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了抛物线的定义及椭圆的几何性质。为求直线AC的方程,本题利利用了待定系数法,通过联立方程组,应用韦达定理,确定了AC、BD的中点坐标,代人已知方程,得到“待定系数”,达到了解题目的。


科目:高中数学 来源:2013届河北省高二下学期一调考试理科数学 题型:解答题
(本题12分)已知圆C的圆心为C(m,0),(m<3),半径为 ,圆C与椭圆E:
,圆C与椭圆E:  有一个公共点A(3,1),
有一个公共点A(3,1), 分别是椭圆的左、右焦点;
分别是椭圆的左、右焦点;
(Ⅰ)求圆C的标准方程;
(Ⅱ)若点P的坐标为(4,4),试探究斜率为k的直线 与圆C能否相切,若能,求出椭
与圆C能否相切,若能,求出椭
圆E和直线 的方程,若不能,请说明理由。
的方程,若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com