
【题目】天气预报说,在今后的三天中,每一天下雨的概率为![]() ,用随机模拟的方法估计这三天中恰有两天下雨的概率.可利用计算机产生0到9之间的整数值的随机数,如果我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,顺次产生的随机数如下:
,用随机模拟的方法估计这三天中恰有两天下雨的概率.可利用计算机产生0到9之间的整数值的随机数,如果我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,顺次产生的随机数如下:
90 79 66 19 19 25 27 19 32 81 24 58 56 96 83
43 12 57 39 30 27 55 64 88 73 01 13 13 79 89
,这三天中恰有两天下雨的概率约为______.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,准线为
,准线为![]() ,若点
,若点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() 是周长为12的等边三角形.
是周长为12的等边三角形.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)设过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 斜率的取值范围.
斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了了解市民搭乘公共交通工具的出行情况,收集并整理了2017年全年每月公交和地铁载客量的数据,绘制了下面的折线图:
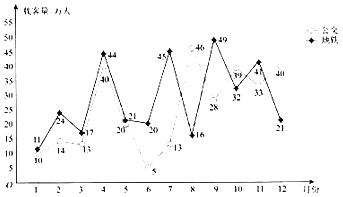
根据该折线图,下列结论错误的是( )
A.全年各月公交载客量的极差为41B.全年各月地铁载客量的中位数为22.5
C.7月份公交与地铁的载客量相差最多D.全年地铁载客量要小于公交载客量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区拟将一半径为![]() 的半圆形绿地改建为等腰梯形
的半圆形绿地改建为等腰梯形![]() (如图,其中
(如图,其中![]() 为圆心,点
为圆心,点![]() 在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设
在半圆上)的放养观赏鱼的鱼池,周围四边建成观鱼长廊(宽度忽略不计).设![]() ,鱼池面积为
,鱼池面积为![]() (单位:
(单位:![]() ).
).
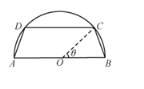
(1)求S关于![]() 的函数表达式,并求鱼池面积何时最大;
的函数表达式,并求鱼池面积何时最大;
(2)已知鱼池造价为每平方米2000元,长廊造价为每米3000元,问此次改建的最高造价不超过多少?(取![]() 计算)
计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com