
【题目】在△ABC中,内角A,B,C所对的边分别为a、b、c,已知a=csinB+bcosC.
(1)求A+C的值;
(2)若b= ![]() ,求△ABC面积的最值.
,求△ABC面积的最值.
【答案】
(1)解:由正弦定理得到:sinA=sinCsinB+sinBcosC,
因为在三角形中,sinA=sin[π﹣(B+C)]=sin(B+C),
所以sin(B+C)=sinBcosC+cosBsinC=sinCsinB+sinBcosC,
所以cosBsinC=sinCsinB,
因为C∈(0,π),sinC≠0,
所以cosB=sinB,即tanB=1,
因为B∈(0,π),
所以B= ![]() ,即A+C=
,即A+C= ![]()
(2)解:由余弦定理得到:b2=a2+c2﹣2accosB,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,当且仅当a=c即
,当且仅当a=c即 ![]() 时“=”成立.
时“=”成立.
而 ![]() ,
,
所以△ABC面积的最大值为 ![]()
【解析】(1)由正弦定理,三角形内角和定理,三角函数恒等变换的应用化简已知可得cosBsinC=sinCsinB,由于sinC≠0,可求tanB=1,结合范围B∈(0,π),即可得解A+C的值.(2)由已知及余弦定理可求 ![]() ,利用基本不等式可求
,利用基本不等式可求 ![]() ,利用三角形面积公式可求△ABC面积的最大值.
,利用三角形面积公式可求△ABC面积的最大值.
【考点精析】利用正弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏有这样一个环节:该关卡有一道上了锁的门,要想通过该关卡,要拿到门前密码箱里的钥匙,才能开门过关.但是密码箱需要一个密码才能打开,并且3次密码尝试错误,该密码箱被锁定,从而闯关失败.某人到达该关卡时,已经找到了可能打开密码箱的6个密码(其中只有一个能打开密码箱),他决定从中随机地选择1个密码进行尝试.若密码正确,则通关成功;否则继续尝试,直至密码箱被锁定.
(1)求这个人闯关失败的概率;
(2)设该人尝试密码的次数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥A-BCDE中,底面BCDE为直角梯形,CD⊥平面ABC,侧面ABC是等腰直角三角形,∠EBC=∠ABC=90°,BC=CD=2BE=2,点M是棱AD的中点

(I)证明:平面AED⊥平面ACD;
(Ⅱ)求锐二面角B-CM-A的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆E的方程;
(2)如图,设椭圆E的上、下顶点分别为A1、A2 , P是椭圆上异于A1、A2的任意一点,直线PA1、PA2分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值. 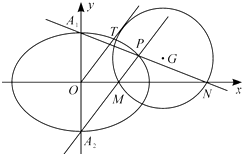
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,有下面结论:

①AC∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1与底面ABCD所成角的正切值是![]() ;
;
④AD1与BD为异面直线.其中正确的结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
,曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直.
(1)求a的值;
(2)若x∈[1,+∞),f(x)≤m(x﹣1)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
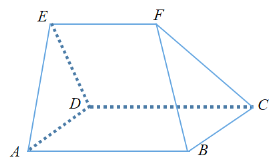
【题目】如图几何体![]() 中,等边三角形
中,等边三角形![]() 所在平面垂直于矩形
所在平面垂直于矩形![]() 所在平面,又知
所在平面,又知![]() ,
,![]() //
//![]() .
.
(1)若![]() 的中点为
的中点为![]() ,
,![]() 在线段
在线段![]() 上,
上,![]() //平面
//平面![]() ,求
,求![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成二面角
所成二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值;
的正弦值;
(3)若![]() 中点为
中点为![]() ,
,![]() ,求
,求![]() 在平面
在平面![]() 上的正投影。
上的正投影。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com